Die Flugbahn einer Kugel: Berechne die Stoßweite. Wie weit ist die Kugel vom Abstoßpunkt entfernt?

Question

Die Flugbahn einer Kugel beim Kugelstoßen wird beschrieben durch den Graphen der Funktion \( f \) mit \( f(x)=-0,08 x^{2}+0,56 x+1,44 \quad(x \) und \( f(x) \) in \( m) \).

a) Berechne die Stoßweite.

b) Kurz vor dem Auftreffen ist die Kugel wieder so hoch wie beim Abstoß. Wie weit ist sie dann vom Abstoßpunkt entfernt?

Ich verstehe diese Aufgabe nicht, kann jemand mir die Rechenwege zerigen und die Rechnung erklären.

Answer 1

Skizze

 

Berechne die Stoßweite.

f(x) = - 0.08·x^2 + 0.56·x + 1.44 = 0   | Lösen mit abc-Formel
x = 9 (∨ x = -2)

 

Kurz vorm Auftreffen ist die Kugel wieder so hoch wie beim Abstoß. Wie weit ist sie dann vom Abstoßpunkt entfehrnt?

f(x) = - 0.08·x^2 + 0.56·x + 1.44 = 1.44
- 0.08·x^2 + 0.56·x = 0
x = 7 (∨ x = 0)

Answer 2

hi

gleichung der flugbahn: f(x) = -0.08x^2 + 0.56x + 1.44
x ist der weg in x-richtung vom koordinatenursprung in meter.
f(x) ist die höhe, abhängig von x.

gesucht ist die wurfweite, dann ist f(x) = 0
die gleichung wird f(x) = 0 gesetzt:

-0.08x^2 + 0.56 + 1.44 = 0

vorbereitung für die pq formel

-0.08x^2 + 0.56x + 1.44 = 0 | : (-0.08)
x^2 - 7x + 1.44 = 0

anwendung der pq formel

x1,2 = 7/2 +- √(49/4 + 72/4)
x1,2 = 7/2 +- √(121/4)
x1,2 = 7/2 +- 11/2
x1 = 18/2 = 9
x2 < 0 -> keine lösung

die wurfweite beträgt 9m

wenn die kugel so hoch wie beim abstoß ist, hat sie beim herabsinken
die höhe 1.44 meter erreicht. das ist die abwurfhöhe.
die abwurfhöhe kann man an der funktion f(x) ablesen.
wir setzen f(x) = 1.44

-0.08x^2 + 0.56x + 1.44 = 1.44 | -1.44
-0.08x^2 + 0.56x = 0 | : (-0.08)
x^2 - 7x = 0
x(x-7) = 0
x = 7

bei x = 7m hat die kugel die höhe 1.44m

p.s.

wenn man die entfernung vom abstoßpunkt (0, 1.44) unbedingt
auch noch wissen will, kann man sie leicht über den satz des
pythagoras berechnen.

lg

Comments

p.p.s

"wenn man die entfernung vom abstoßpunkt (0, 1.44) unbedingt
auch noch wissen will, kann man sie leicht über den satz des
pythagoras berechnen."

das ist natürlich quatsch :D

kann gestrichen werden, danke :-)

mfg

    gorgar

Answer 3

a) Finde y = 0. Dafür mit -0,08 dividieren und die pq-Formel verwenden.

-0,08x^2+0,56x+1,44 = 0    |:(-0,08)

x^2-7x-18 = 0     |p = -7 und q = -18

x₁ = -2 und x₂ = 9

Folglich liegt eine Stoßweite von 9 m vor (denn wir werfen ja ab x = 0).

b) Bestimme y = 1,44

-0,08x^2+0,56x+1,44 = 1,44  |-1,44

-0,08x^2+0,56x = 0

-0,08x(x-7) = 0

x₃ = 0 und x₄ = 7

Das ist also in einer Entfernung von 7 m der Fall.

Grüße

Answer 4

f(x) = -0,08x² + 0,56x + 1,44

Kurz vor dem Auftreffen ist die Kugel wieder so hoch wie beim Abstoß. Wie weit ist sie dann vom Abstoßpunkt entfernt?

Beim Abstoß hat die Kugel offensichtlich die Höhe

f(0) = -0,08*0² + 0,56 * 0 * 1,44 = 1,44

An welcher Stelle hat sie also ein weiteres Mal diese Höhe?

f(x) = -0,08x² + 0,56x + 1,44 = 1,44

-0,08x² + 0,56x = 0 | x ausklammern

x * (-0,08x + 0,56) = 0

x₁ = 0

-0,08x + 0,56 = 0

-0,08x = - 0,56 | : (-0,08)

x₂ = 7

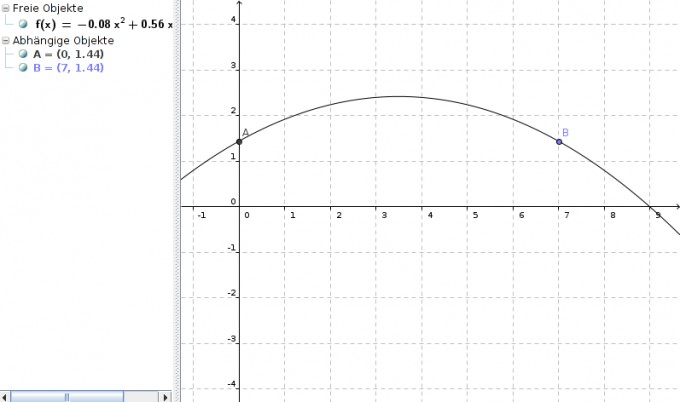
Nach 7 Metern hat die Kugel also die gleiche Höhe wie beim Abstoß:

Besten Gruß

Comments

Vielen Dank erstmal, doch eine Frage habe ich noch: Woher kann man erkennen, dass y=1,44 ist,also dass die Kugel aus einer Höhe von 1,44 Metern abgeworfen wird? Für mich ist 1,44 die Q vom PQ Formel. In der Klausur würde ich wahrscheinlich nicht weiterkommen, weil ich nicht begründen kann, warum 1, 44 die Höhe ist, aus der der Werfer die Kugel wirft.

---

Mit der pq-Formel hat das nichts zu tun, denn wie man einen Punkt benennt, ist völlig willkürlich :-)

Der Kugelstoßer steht sozusagen am Koordinatenursprung (siehe Skizze), seine Füße befinden sich also am Punkt (0|0). Wenn man also für x = 0 wählt, ergibt sich: f(0) = 1,44. Das ist dann offensichtlich die Höhe, an der der Kugelstoßer die Kugel hält und abstößt.

---

Also könnte man quasi sagen, dass y = 1,44 ist' weil die anderen Zahlen in der Gleichung die Variabel x haben. Dadurch bleibt für Y nur 1,44, da 1,44 keine Variabel hat. Habe ich es richtig verstanden? Vorab: Vielen Dank, dass Sie sich die Zeit für so einen dummen Schüler wie mich nehmen xD

---

Keine Ursache, sich zu bedanken :-)

Mathematisch korrekter wäre vielleicht die Aussage:

f(0) = 1,44

Irgendeine Variable x muss man schon in die gegebene Funktionsgleichung eingeben, denn letztere ist ja eine Funktion von x.

Und wenn wir 0 für x einsetzen - also die Stelle, an der der Abstoß erfolgt -, kommen wir auf

f(x) = -0,08x² + 0,56x + 1,44, also

f(0) = -0,08 * 0² + 0,56 * 0 + 1,44 = 1,44

Schau Dir vielleicht zum besseren Verständnis nochmals die Skizze an, setze einige Werte für x ein, berechne dann f(x) und vergleiche sie mit den Punkten in der Skizze. Dann wird Dir sicherlich alles ein wenig klarer :-)