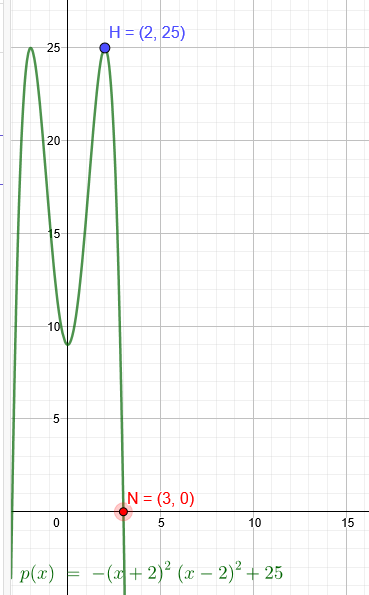
"Gesucht ist eine ganzrationale Funktion 4. Grades. Der Graph ist zur y-Achse symmetrisch, hat im Punkt H (2 | 25) einen Hochpunkt und schneidet die x-Achse an der Stelle x = 3"
Wegen der Achsensymmetrie liegt ein 2. Hochpunkt bei M(-2 | 25)
Ich verschiebe den Graphen um 25 Einheiten nach unten und löse mit der Nullstellenform der Parabel 4.Grades.
\(f(x)=a*(x+2)^2*(x-2)^2\)
N(3|0)→N´(3|-25)
\(f(3)=a*(3+2)^2*(3-2)^2=25a→25a=-25→a=-1\)
\(f(x)=-(x+2)^2*(x-2)^2\)
Nun 25 Einheiten nach oben:
\(p(x)=-(x+2)^2*(x-2)^2+25\)