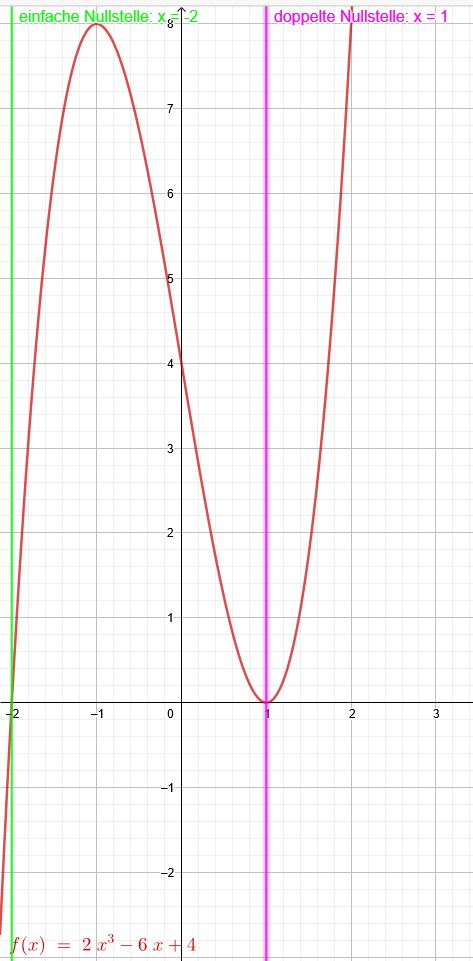
\(y=2x^3-6x+4\) Da hier eine ausführliche Kurvendiskussion ansteht, ist es günstig, zuerst die Extremstellen zu suchen:
\(y'=6x^2-6\) \(6x^2-6=0\)
\(x_1=1\) \(y(1)=2-6+4=0 \)
\(x_2=-1\) \(y(-1)=-2+6+4=8 \)
Da nun an der Stelle \(x=1\) ein Extremwert gefunden ist, existiert dort eine doppelte Nullstelle.
Nächste Nullstelle über die Polynomdivision:
\((2x^3-6x+4):(x-1)^2\)
\((2x^3-6x+4):(x^2-2x+1)=2x+4\)
\(2x+4=0\)
\(x_3=-2\)