ich hab ein folgendes Problem und komme nicht weiter.
Die Aufgabe lautet:
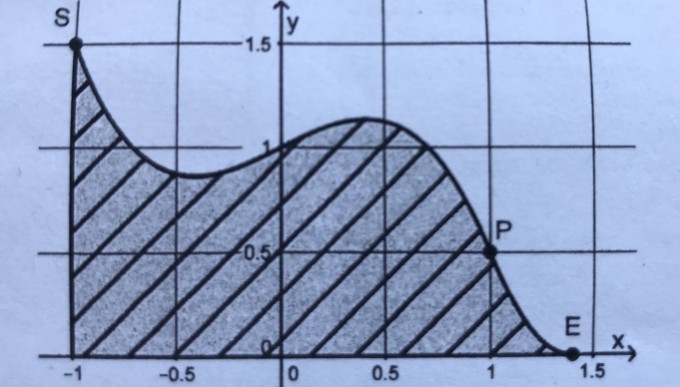
Die folgende Abbildung stellt einen Entwurf für das Profil einer Kugelbahn dar. (Anhang)
Für die Modellierung werden die folgenden Funktionen f und g verwendet:
f(x) = -x3 + 0,5x + 1 für den Bereich -1 ≤ x ≤ 1 und g(x) = ax2 + bx + 6,25 für den Bereich 1 ≤ x ≤ 1,4
x in Metern, f(x) und g(x) in Höhe über dem Boden in Metern. Der waagerechte Boden ist durch die x-Achse gegeben.
a) Bestimmen Sie die Werte für die Parameter a und b so, dass der Übergang im Punkt P(1 I 0,5) sprung- und knickfrei ist.
(Zur Kontrolle a = 3,125 und b= -8,75)
Problem/Ansatz:
Ich verstehe wie die Bedingungen für die Funktionen lauten, damit zwei Graphen sprung- und knickfrei sind. Hier habe ich zuerst f(1) eingesetzt (da es ja einer der beiden Bedingungen ist). Es kommt wie erwartet 0,5 raus. Dem entsprechend müsste ich ja auch g(1) berechnen, um auch auf den y-Wert 0,5 zu kommen, aber hier stellt sich nun auch meine Frage. Ich habe zwei Parameter (a und b) und komme bei der Berechnung dafür nicht klar. Vielleicht gehe ich das auch alles falsch an?
g(1)
0,5 = a · 1^2 + b · 1 + 6,125 I -6,125
-5.625 - b = a · 1^2
Und ab hier habe ich nicht weiter gerechnet, weil es meiner Meinung nach keinen Sinn ergab
Ich denke ihr könnt mir dabei helfen !:)
Mit freundlichen Grüßen