Ich habe mal eine Lösung unter folgendem Link bereitgestellt: https://docs.google.com/document/d/1UietaqhnJDiiyYtv3feZwmaArib13BxPMIWFHS-SEXQ/pub
Kurvenschar fa(x) = a·x + e^{-x} , a > 0
a) Berechnen Sie fa'(x) und fa''(x).
fa(x) = a·x + e^{-x}
fa'(x) = a - e^{-x}
fa''(x) = e^{-x}
b) Berechnen Sie Extrem- und Wendepunkte.
Extremstellen fa'(x) = 0
a - e^{-x} = 0
x = - ln(a)
fa(- ln(a)) = a - a·ln(a)
fa''(- ln(a)) = a > 0 --> Tiefpunkt
Wendestellen fa''(x) = 0
e^{-x} = 0
Die e-Funktion wird nie Null, daher gibt es keine Wendepunkte.
c) Skizzieren Sie den Graphen für f1 und f2 im Intervall -2 ≤ x ≤ 3.
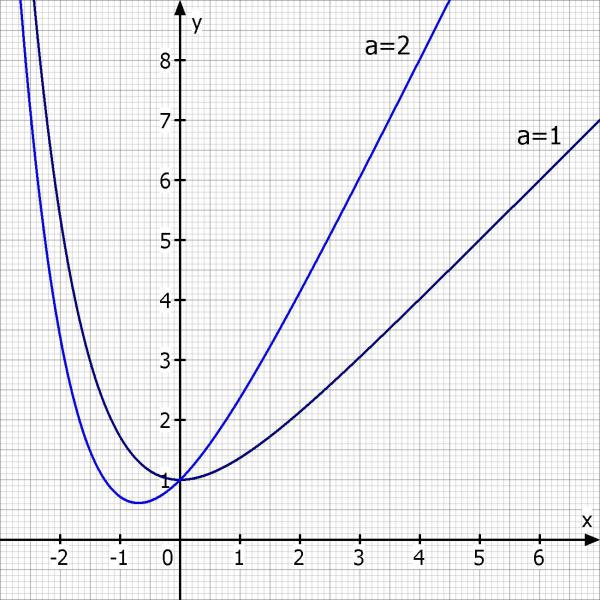
d) Wie lautet die Tangente an fa im Schnittpunkt mit der Y-Achse?
xs = 0
fa(xs) = fa(0) = 1
fa'(xs) = fa'(0) = a - 1
t(x) = fa'(xs)·(x - xs) + fa(xs) = (a - 1)·(x - 0) + 1 = (a - 1)·x + 1
e) Bestimme eine Stammfunktion Fa von fa.
fa(x) = a·x + e^{-x}
Fa(x) = 1/2·a·x^2 - e^{-x}
f) Gesucht ist der Inhalt der Fläche Aa , die im 1. Quadranten zwischen dem Graphen fa und dem Graphen ga(x) = a + e^{-x} und der Y-Achse liegt. Für welchen Wert von a hat diese Fläche den Inhalt 1?
da(x) = ga(x) - fa(x) = (a + e^{-x}) - (a·x + e^{-x}) = a - a·x
Da(x) = a·x - a/2·x^2
da(x) = 0
a - a·x = 0
x = 1
∫ (0 bis 1) da(x) dx = Da(1) - Da(0) = a/2 = 1
a = 2
