Kurz nachdem Ramanujan in England angekommen war, stellt er den Lesern einer Mathematik-Fachzeitschrift die Frage nach dem Wert von
\( \sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{1+...}}}} \)
Auch Monate später hatte niemand geantwortet. Heute – im Zeitalter elektronischer Werkzeuge – ist es leicht, eine Hypothese zu formulieren und diese anschließend zu erhärten. Dazu wird die Kettenwurzel immer wieder an einer Stelle abgebrochen, an der ein Malpunkt steht. Es wird also diese Folge betrachtet:
\( \sqrt{1+2} \) , \( \sqrt{1+2\sqrt{1+3}} \) , \( \sqrt{1+2\sqrt{1+3\sqrt{1+4}}} \) , und so weiter.
Dann erhalten wir (gerundet) diese Wertetabelle:
| Erste nicht berechnete Wurzel hinter | 2
| 3
| 4
| 5
| 6
| 7
| 8
|
| Wert der abbrechenden Kettenwurzel | 1,73
| 2,23
| 2,559
| 2,755
| 2,867
| 2,929
| 2,962
|
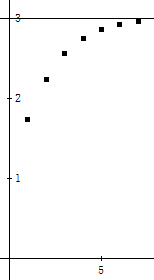
Ihr Graph führt zu der Hypothese, dass der gesuchte Wert der Kettenwurzel 3 sei.
Den Ansatz \( \sqrt{1+2\sqrt{1+3\sqrt{1+4\sqrt{1+...}}}} \) =3 kann man umformen zu \( \sqrt{1+3\sqrt{1+4\sqrt{1+...}}} \) =4 und dann zu \( \sqrt{1+4\sqrt{1+...}} \) =5
und allgemein zu \( \sqrt{1+n\sqrt{1+(n+1)\sqrt{1+(n+2)\sqrt{1+...}}}} \) = n+1.
Diese Formel könnte man durch vollständige Induktion beweisen.
Induktionsvoraussetzung: \( \sqrt{1+n\sqrt{1+(n+1)\sqrt{1+(n+2)\sqrt{1+...}}}} \) = n+1.
Beide Seiten (erstens) quadrieren, (zweitens) 1 subtrahieren, (drittens) durch n dividieren, ergibt die Induktionsbehauptung. Da der Induktionsanfang jedoch die zu beweisende Formel selbst ist, liegt jetzt ein Zirkelschluss vor. Deshalb soll skizziert werden, wie Ramanujan selbst den Beweis führte. Vorausgeschickt sei, dass Ramanujan auf einen Existenzbeweis verzichtete. Aber sein Vorgehen war so trickreich, dass sich ein Blick darauf lohnt.
Ramanujans Ausgangspunkt war die in ℕ allgemeingültige Formel (*) n·(n+2)=n·\( \sqrt{1+(n+1)(n+3)} \). Sodann definierte Ramanujan eine Funktion f mit der Gleichung f(n)=n·(n+2) und berechnete dazu die Funktionswerte f(n+1), f(n+2),f(n+3) und so weiter, die er dank (*) in zwei verschiedenen Versionen angeben konnte. Durch sukzessives Einsetzen der soeben gewonnenen Gleichungen ineinander bewies Ramanujan die Gültigkeit der Formel
f(n)=n·\( \sqrt{1+(n+1)\sqrt{1+(n+2)√1+(n+3)\sqrt{1+...}}} \)
Daraus gewann er dann die gesuchte Lösung seiner Aufgabe.