Integration durch Substitution

Question

ich übe grade Integration und möchte folgende Aufgabe lösen:

$$\int_{0}^{2}(t+2) \sin \left(t^{2}+4 t-6\right) d t$$

und hier ist meine Ansatz:

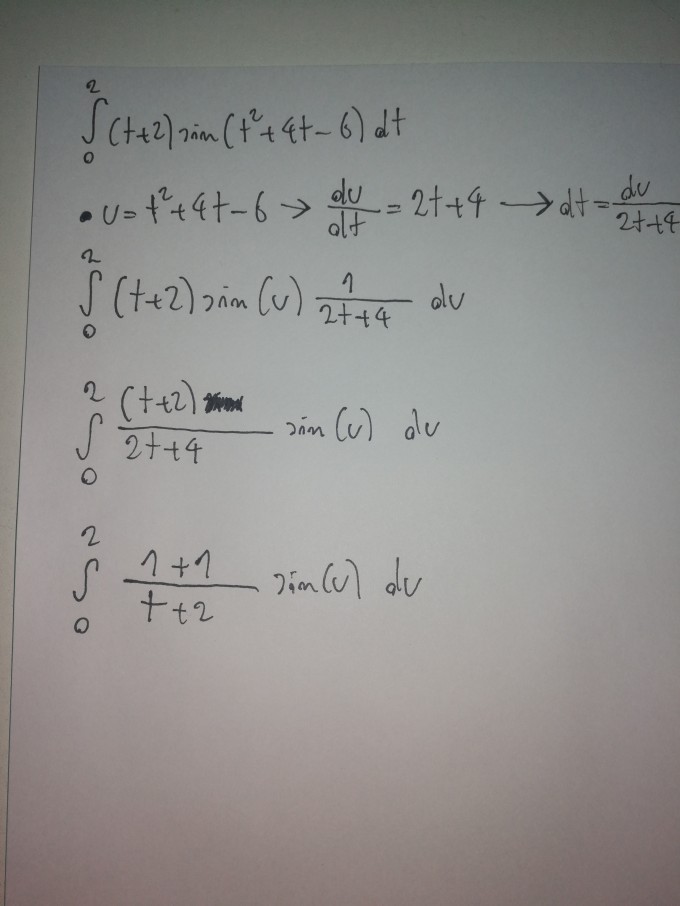
aber laut Integralrechner kommt man auf Zwischenschritt:

$$=\int \frac{\sin (u)}{2} \mathrm{d} u$$

Kann jemand bitte erklären wie man darauf kommt?

Answer 1

Achtung: (t + 2)/(2·t + 4) ≠ (1 + 1)/(t + 2) !!!

(t + 2)/(2·t + 4)
= (t + 2)/(2·(t + 2))
= 1/(2·1)
= 1/2

Noch ein anderer Fehler ist, das du offensichtlich die Integrationsgrenzen nicht mit substituiert hast. Das müsste beim Übergang von dt nach du gemacht werden.

Comments

ah stimmt, ich hab mich vertan, vielen Dank!!!