Bestimmen Sie das Supremum, Infimum, Maximum und Minimum

Question

Man muss das Supremum, Infimum, Maximum und Minimum bettimen von M = 1/x + 3cos(x-1)  x∈R>=1

Ich hab die ableitung f'(x) -1/x^2 -3sin(1-x) aber ich weiss nicht wie man daraus jetzt das max betimmen kann.

Bitte hilfe.

Answer 1

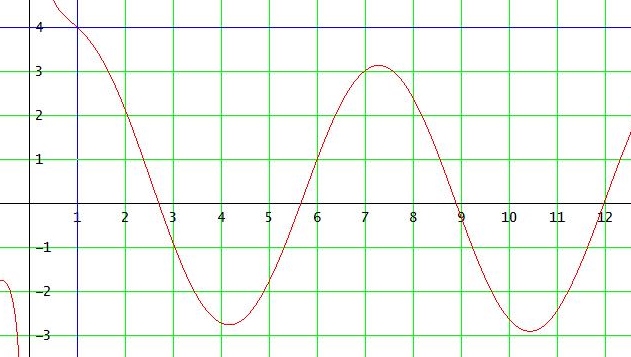
M = { 1/x + 3cos(x-1) | x ∈ ℝ_≥1 }

der Wert des Summanden  3cos(x-1) schwankt mit der Periode 2π im Intervall [-3 , 3].

       Er hat ein Maximum (3) für x-1=0, also für x=1.

Der Wert des Summanden 1/x ist streng monoton fallend, hat sein Maximum 1 für x=1

                  und lim_x→∞ 1/x = 0.

→  M hat das Maximum (=Supremum)  1+3 =4 und das Infimum -3  (kein Minimum).

Gruß Wolfgang