Du hast \(z=3-5i\). Daher ist \(\Re(z)=3\) und \(\Im(z)=-5\). Ferner ist \(|z|=\sqrt{34}\).
Die Polardarstellung ist \(z=r\cdot e^{i\cdot \varphi}\), wobei \(r=|z|\) und \(\varphi=\arg(z)\). Hierbei ist \(\arg(z)\) die Argument-Funktion.
Geometrisch in der gaußschen Zahlenebene ist das aber eigentlich ganz leicht zu bestimmen.
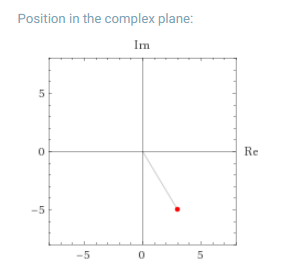
Hier ist \(\varphi\) der Winkel zwischen der Ordinate (Imaginärachse) und dem Ursprung. Und die Länge hast du oben via Pythagoras.
Insgesamt erhalte ich \(z=\sqrt{34}\cdot e^{-i\cdot \arctan\left(\frac{5}{3}\right) }\)