Die Gesamtarbeitszeit von Maschine A und B
ist 1200.
2x1 + 4x2 ≤ 1200
5x1 + 1x2 ≤ 1200
gewohnter
2x + 4y ≤ 1200
5x + y ≤ 1200
umstellen und nur die Geradengleichung
4y = 1200 - 2x
y = 300 - 0.5x
y = 1200 - 5x
Gezeichnet
y = 300 - 0.5x
y = 1200 - 5x
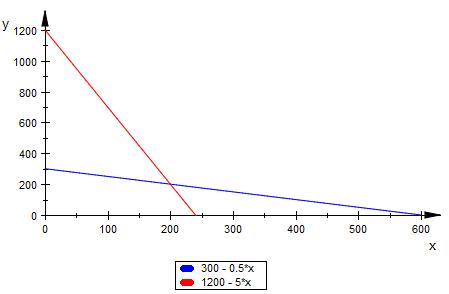
Für die Lösungsfläche gilt
( unterhalb von blau und unterhalb von rot )
y ≤ 300 - 0.5x
y ≤ 1200 - 5x
Dies ist die Schnittfläche des linken Dreiecks.
Eckpunkte
( 240 | 0 )
( 200 | 200 )
( 600 | 0 )
Gewinne rechnerisch
240 * 8 + 0 * 6 = 1920
200 * 8 + 200 * 6 = 2800
600 * 8 + 0 * 6 = 4800
Müßte stimmen.
Die rein zeichnerische Lösung mit Einzeichnung
der Gewinngeraden kann nachgeliefert werden.
mfg Georg