man könnte so vorgehen, obwohl das sicher nicht die eleganteste Lösung ist:
1. Die Strecke UE mit dem Satz es Pythagoras berechnen, daraus ergibt sich dann die Strecke ME mit 7,32
2. Die Strecke IE ergibt sich aus \( \frac{7,32}{sin(60)} \) = 8,45
3. Die Strecke IM kann mit Pythagoras berechnet werden = 4,23
4. Zur Berechnung der Strecke FI = 7,2 habe ich diesen Rechner benutzt:
https://www.arndt-bruenner.de/mathe/scripts/dreiecksrechner.htm
mit den Eingaben IM = a = 4,23, Gamma = 120° und c = FM = 10
5. Strecke EF = 7,2 + 8,45 = 15,65
6. HE = cos(30°) · 15,65 = 13,55
7. HM = 13,55 - 7,32 = 6,23
8. Die Hälfte des Winkels bei M ist cos-1 von 6,23 : 10 = 51,46, der ganze Winkel hat also 102,93 ° 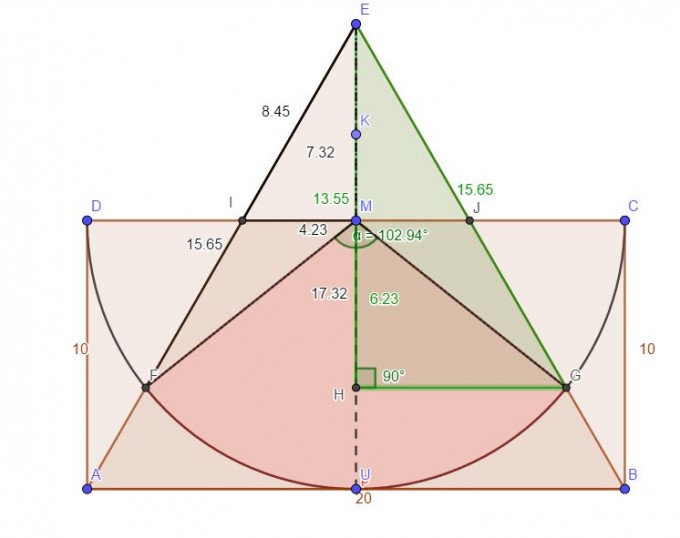
Gruß, Silvia