Hallo Anna,
Lauteten die Ebenengleichungen $$E: \quad 2x_1 - x_2 + 5x_3 = 7\\ F: \space 4x_1 - 2x_2 +10x_3 = 18$$so kann man das in Vektorschreibweise wie folgt schreiben$$E: \quad \begin{pmatrix} 2\\ -1 \\ 5\end{pmatrix} x = 7; \quad \quad F: \quad \begin{pmatrix} 4\\ -2 \\ 10\end{pmatrix} x = 18$$Der Vektor vorn ist der Normalenvektor der Ebene. Dieser Vektor steht senkrecht auf der Ebene.
Ich habe die beiden Ebenen inklusive ihrer Normalvektoren in Geoknecht3D eingezeichnet.
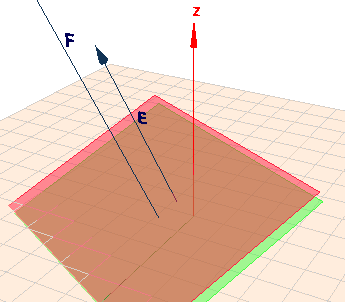
Wie Du siehst, sehen die beiden Ebenen parallel aus. Und sie sind genau dann parallel, falls ihre beiden Normalvektoren in die gleiche Richtung zeigen. Dazu muss einer von ihnen ein Vielfaches des anderen sein, d.h. es muss gelten$$ \begin{pmatrix} 2\\ -1 \\ 5\end{pmatrix} = f \cdot \begin{pmatrix} 4\\ -2 \\ 10\end{pmatrix}$$Das ist hier der Fall! Für \(f=2\) geht obige Gleichung aus. Daraus folgt, dass die beiden Normalvektoren kolinear und die Ebenen parallel sind.
Gruß Werner