Die Ebene ist gegeben durch E: 2x1-x2+2x3=10

Question

Bestimme den Abstand des Punktes -2/3/4. Nun meine Frage man bekommt ja dann -9/3, dass gibt ja -3. Aber mein Lehrer kommt auf +3? Mir ist das jetzt schon öfters bei dieser Art von Rechnung aufgefallen, dass ich immer - bekomme er aber +. Kann mir jemand sagen, was ich falsch rechne?

Comments

Was soll denn ein negativer Abstand sein?

Answer 1

Aloha :)

Ein Normalenvektor der Ebene ist hier:$$\vec n=\left(\begin{array}{c}2\\-1\\2\end{array}\right)$$Der Abstand des Punktes \(P(-2|3|4)\) von der Ebene beträgt also:$$d=\left|\frac{\vec n\cdot\vec p-10}{|\vec n|}\right|=\left|\frac{\left(\begin{array}{c}2\\-1\\2\end{array}\right)\cdot\left(\begin{array}{c}-2\\3\\4\end{array}\right)-10}{\sqrt{2^2+(-1)^2+2^2}}\right|=\left|\frac{1-10}{3}\right|=\left|\frac{-9}{3}\right|=3$$In der Formel wird der Abstand durch die Betragsstriche immer \(\ge0\). Hast du vor der Betragsbildung ein positives Ergebnis, dann liegt der Punkt in Richtung des Normalenvektors "über" der Ebene. Ist das Ergebnis vor der Betragsbildung negativ, dann liegt der Punkt in Gegenrichtung des Normalenvektors "unter" der Ebene. Aber der Abstand ist in beiden Fällen derselbe, daher nimmt man den Betrag.

Comments

aber -15/3 gibt doch -3 nicht 3?

---

Stimmt, du hast mich ganz durcheinander gebracht ;))) Es gibt  vor allen Dingen \(-5\). Ich hatte einen Fehler im Skalarprodukt. Ich habe es korrigiert...

Answer 2

man bekommt ja dann -9/3, dass gibt ja -3.

Wie bist du denn auf -3 gekommen?

Hessesche Normalenform?

Ganz gleich, welche Formel du verwendet hast: sollten in deiner Formel nicht irgendwelche Betragsstriche gewesen sein, die du möglicherweise ignoriert hast?

Comments

ja ich habe die hessesche normalenorm benützt also

2*(-2)-1(3)+2*(4)-10= -9

dann Wurzel 2^2+(-1)^2+(2)2= 3

gibt doch -3?

Answer 3

Hallo Anna,

nochmal zum Verständnis: Ich habe Dir die Ebene \(E\) und den Punkt \(P\) nebst seiner Projektion \(P'\) auf \(E\) im Geoknecht3D eingegeben

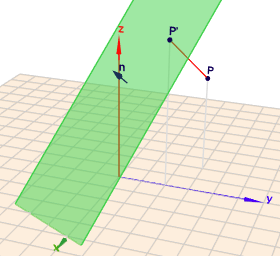
(klick auf das Bild, und rotiere die Szene mit der Maus)

liegt \(P\) auf der vom Vektor \(n\) abgewandten Seite - so wie in diesem Fall - so bekommst Du einen negativen Wert für den Abstand \(e\) mit $$e = n \cdot P - d = \frac 13 \left(  \begin{pmatrix}2\\ -1\\ 2\end{pmatrix} \cdot \begin{pmatrix}-2\\ 3\\ 4\end{pmatrix} - 10  \right) = -3$$Würde der Punkt \(P\) auf der anderen Seite liegen, so wäre der Wert positiv.

Da dies für die Abstandsberechnung oft irrelavant ist, wählt man dann den Betrag dieses Wertes.