Aufgabe:
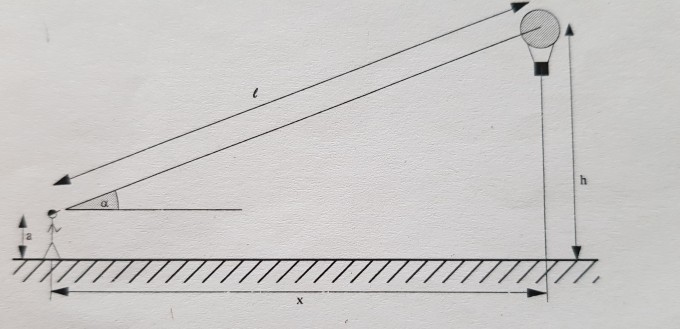
Ein Freiluftballon fährt in einer Höhe von 375m. Er wird unter einem Erhebungswinkel alpha=25.2° von einem Begleiter (Augehöhe a = 1,8m) beobachtet.
Berechnen Sie die Entfernung l des Ballons
Problem/Ansatz:
Meine Rechnung:
h1 = h - a = 373.2m
sin(25.2) = h1 \ l | : h1 | Kehrwert
h1 / sin(25.2) = l
373.2 / sin(25.2) = 877.22m
für x habe ich den Pythagoras benutzt und 793,87m raus.
Richtig?