Grenzwert bestimmen: lim_(x->1) (4x^2 - 4) / (1-x)

Question

Aufgabe:

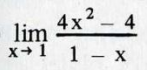
Problem/Ansatz:

Die Lösung ist 8.

Nur kann ich diese Lösung nicht nachvollziehen , da :

Beid er Grenzwertberechnung setzt man doch den "Grenzwert"  x ein und guckt in welche Richtung die Funktion konvergiert.

In diesem Falle komme ich (setze die 1 ein, da gegeben ) auf 0.

Ich bitte um eine Erklärung.

Danke

Comments

Du dividierst durch null?

Answer 1

lim_(x->1) (4x^2 - 4) / (1-x)           

= lim_(x->1) (-4(1 - x^2 )) / (1-x)      | 3. binomische Formel

= lim_(x->1) (-4(1 - x)(1+x )) / (1-x)         | kürzen

= lim_(x->1) (-4(1+x )) , x≠1

= -4 (1+1)

= -8 

Kann die vorgegebene Antwort nicht bestätigen.

https://www.wolframalpha.com/input/?i=lim_(x-%3E1)+(4x%5E2+-+4)+%2F+(1-x)

kommt auch auf "Minus 8".

Comments

Es sollten -8 und nicht 8 sein.Danke dir.

Das man net durch 0 teilen kann weiß ich.

Also muss man die Funktion so umformen , dass der Nenner net 0 ist oder?

---

Jein. Der Nenner Null ist von Anfang an verboten. D.h. der Bruchtterm hat an der Stelle x = 1 eine Definitonslücke.

Links und rechts von der Definitionslücke entspricht der Bruchterm

(-4(1+x ))

Die Ergänzung x≠1 gehört nur deshalb dazu, weil man zu Beginn der Umformung x = 1 nicht einsetzen durfte. Der zugehörige Graph hat an dieser Stelle ein Loch. Punkt P(1|-8) fehlt in der zum Term passenden Geraden. 

---

Hatte die Regel von L Hospital vergessen....

Ist mir gerade eingefallen

---

Die brauchst du bei dieser Aufgabe gar nicht, die 3. binomische Formel genügt :) Vgl. meine Antwort.

Aber gut, dass du Hospital nun wieder kennst.

Answer 2

8 ist falsch.

Comments

Es sollten -8 und nicht 8 sein.Danke dir.

Answer 3

Hallo

 beim einsetzen von Null kommst du auf den unbestimmten Ausdruck 0/0 deshalb Darstellung du das gar nicht  klammerst du dagegen oben 4 aus un kennst binomische Formeln, dann steht oben 4*(x+1)*(x-1)

für alle x ungleich 1 kannst du kürzen und dann hast du 4(x+1) übrig auch beliebig nahe an x=1  und kannst JETZT x=1 einsetzen.

Gruß lul

Comments

Das man net durch 0 teilen kann weiß ich.

Also muss man die Funktion so umformen , dass der Nenner net 0 ist oder?(Allg. Vorgehen gemeint)

Danke dir