ich lade dir mal eine Lösungsidee rauf.

Ich hoffe du kannst das obige lesen:
Zu a)
Wenn du deine Vektoren auf lineare Unabhöngigkeit prüfen willst,
dann kannst du sie in eine Matrix packen und mit dem Gaussverfahren diese betreffende Matrix in Zeilenstufenform bringen,
da die Zeilenstufenform gegeben ist, gilt dass sie linear unabhängig sind.
Dieses verfahren eignet sich auch um herauszufinden was das minimale Erzeugendensystem ist (falls ihr das schon hattet).
Zu b)
Mit dem Span von bestimmten Vektoren, also in deinem Fall von den zwei Vektoren v1,v2 heisst, dass
du sehen kannst, was sie aufspannen.
Um zu sehen, was sie Aufspannen führst du eine Linearkombination durch.
In der Aufgabe heisst es, dass du überprüfen sollst, ob sie den Vektor v3 aufspannen, das heisst wiederum, dass es (falls es wirklich stimmt) v1 und v2 linearkombiniert den gesuchten Vektor v3 aufspannen sollen.
⟨v1, v2⟩ = s*v1 + t*v2 = v3.
Beachte dass: t,s sind Elemente aus IR.
Und nun, wenn du das aufgeschrieben hast, kannst du das Gleichungssystem nach einer Variabel s oder t auflösen und durch einsetzen dann die andere Variabel herausfinden.
In meiner Rechnung ergab t = -1 und s = 2, was bedeutet, dass:
s*v1 + t*v2 = v3.
2* (1,1,0) + -1*(-1,2,0) = (3,2,0)
(2,2,0) + (1,-2,0) = (3,2,0)
(3,0,0) ungleich (3,2,0)
Achtung, ich glaube ich habe einen fehler gemacht.... moment...
Korrektur zu b)
Analog wie oben Gleichungssystem auflösen, dann bekommen wir
s = 8/3 und t = -1/3
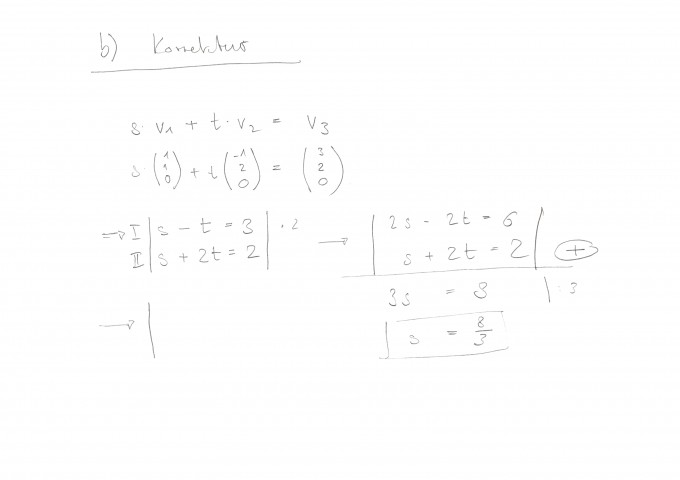
s in eine Gleichung einsetzten und nach t auflösen, liefert t = -1/3.
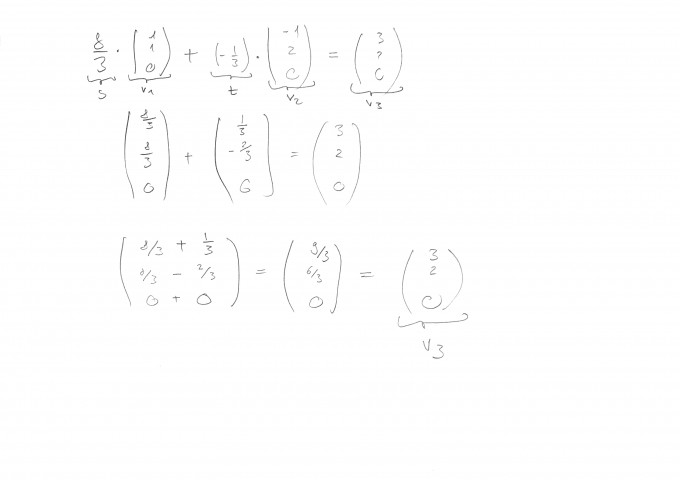
So, jetzt stimmts hoffe ich.