Hallo cinderr,
Du hast ja auf meinen Hinweis mit der Überbestimmtheit bisher nicht reagiert. Vielleicht verrätst Du uns noch aus welchem Kontext die Aufgabe entstammt.
ich möchte es gerne programmieren.
D.h. man kann auch ein iteratives Verfahren wählen, was zwar nicht die Lösung liefert (IMHO gibt es die nicht!), aber immerhin eine Position für \(P\) und einen Wert für \(r\), der die Vorgaben ungefähr erfüllt.
Als Beispiel habe ich ein Rechteck mit den Maßen \(12 \times 7\) gewählt und die Werte für die \(x_i\) sind \(x_1=5\), \(x_2=6\) und \(x_3 =4\). Dann komme ich zu folgendem Bild:
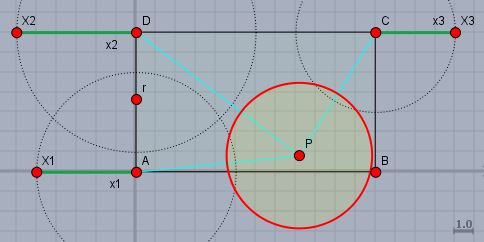
Der Punkt \(A\) liegt im Ursprung und \(B\) bei \(B=(12|\,0)\). Ergebnis: \(P \approx (8,21|\, 0,83)\) und \(r\approx 3,66\). Als Kriterium für den 'best fit' habe ich ein Energieminimum gewählt.
Man kann an diesem Beispiel auch gut sehen, dass es schwerlich eine bessere Lösung gibt. \(P\) ist von \(D\) noch zu weit entfernt. Rückt man ihn aber näher an \(D\), so muss man \(r\) verkleinern, damit die Abstände zu \(A\) und \(C\) passen. Damit entfernt sich \(P\) aber zu weit von \(B\).
Wenn Du mehr dazu wissen möchtest, so melde Dich nochmal.
Lässt man den Punkt \(B\) weg, so handelt es sich um das Problem der Apollonischen Kreise.