n x n Matrizen vollständige induktion

Question

Aufgabe: wir betrachten die n x n matrizen

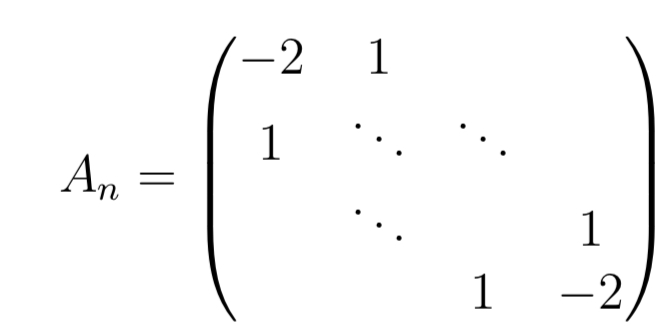
Beweisen sie mit vollständiger induktion und Laplace Entwicklung, dass det(A_n)=(-1)ⁿ(n+1)

Problem/Ansatz:

Bis jetzt habe ich nur dass hier :

Det(An)=Det(An-1)+det(-2)+det(1)+det(n-1)

Nur weiß ich nicht ob mein Ansatz richtig ist bzw. wie ich weitermachen soll.

Wäre um jede Hilfe dankbar

Answer 1

Vielleicht geht es so:

Wenn du det(A_n) nach der 1. Spalte entwickelst, entsteht

det(A_n) = -2*det(A_n-1) - 1 *det (B_n-1)

wobei B_n-1 so aussieht

1        0      0     0     ……………………
1      -2      1      0    ……………………
0       1      -2     1    ……………………..

………………………………………..

       ……………………………………..1

  ……….…………………….        1    -2

und wenn du diese nach der 1. Zeile entwickelst

hast du   det (B_n-1) = 1*det(A_n-2)

also insgesamt

det(An) = -2*det(A_n-1) - det (A_n-2)