Wie hoch ist der Hügel schätzungsweise?

Question

Aufgabe:

Berechne die Höhe des Felsens.

Wäre über eine Lösung sehr dankbar!

LG

Comments

Dein Freund Wolfram ist nur einen Klick entfernt

https://www.wolframalpha.com/input/?i=tan(60%C2%B0)%3Dh%2Fx,tan(49%C…

h≈171.27, x≈98.8829

Answer 1

u/sin(49°)=50/(sin(180°-(180°-60°)-49°)   [1]      | Sinussatz

sin(60°)=x/u   [2]    | Winkelbeziehung im rechtw. Dreieck.

Answer 2

Berechne die Höhe des Felsens.

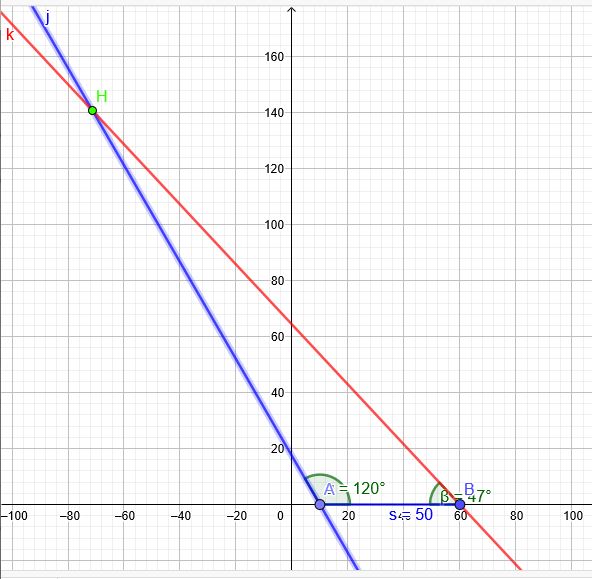
Geradengleichung durch A$(10|0)$ mit der Steigung $m=\tan(120°)=- \sqrt{3}$

$\frac{y}{x-10}=- \sqrt{3}$

$y=- \sqrt{3} x+10\sqrt{3}$

Geradengleichung durch B$(60|0)$ mit der Steigung $m=-\tan(47°)=- 1,072$

$\frac{y}{x-60}=- 1,072$

$y=- 1,072x+64,32$

Beide Geraden schneiden sich auf der Höhe des Felsens:

$- \sqrt{3} x+10\sqrt{3}=- 1,072x+64,32$

$- \sqrt{3} x+1,072x=64,32 -10\sqrt{3}$

$x=-71,21$   $y(-71,21)=- 1,072\cdot (-71,21)+64,32 =140,65$m

Comments

Soll 140,65m die Höhe sein?

---

In Anbetracht der Tatsache, dass andere Benutzer schon vor sechs Jahren die richtige Lösung hingeschrieben haben (mit 49°), kann nicht die Höhe gemeint sein.

---

49° oder 47°, das ist hier die Frage.