Flächenstück zwischen 3 unterschiedlichen Kreisen

Question

Aufgabe:

Drei Kreise mit den Radien r1 = 5cm, r2 = 4cm, r3 = 3cm berühren sich gegenseitig von außen. Wie groß ist das Flächenstück zwischen den 3 Kreisen?

ich weiß, dass es eine Formel gibt und man Werte voneinander abziehen muss. Allerdings habe ich speziell zu meiner Aufgabe kaum was im Internet gefunden, was mir weiterhelfen könnte. Wenn mir jemand die benötigte Formel erklärem bzw. Tipps geben könnte, wäre das sehr nett.

Gruß Mathekoala

Comments

Könnte das eine mögliche Skizze sein (du würdest hier die Lila-Fläche suchen wollen):

---

"berühren sich gegenseitig" bedeutet paarweise!

---

oder vielleicht so?

---

berühren sich gegenseitig von außen

Da kann wohl nur das 2. Bild gemeint sein.

---

Ich versuche es gleich erneut.

---

Ich habe die Aufgabe leider nur in Textform, also keine weiteren Informationen dazu. Und auch keine bildliche Darstellung zu der Aufgabe. Aber denke auch eher, dass es wie die Skizze aussehen soll, die Silvia erstellt hat.

Answer 1

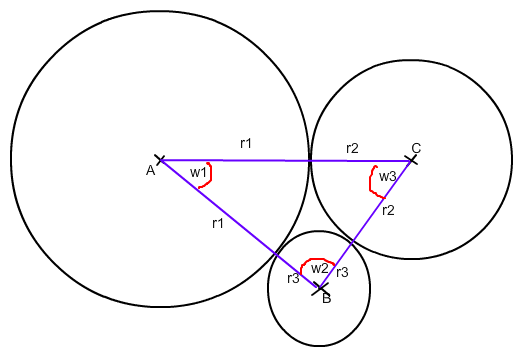
AB = 8 cm  ,  AC = 9 cm ,  BC = 5 cm

Mit dem Kosinussatz (Sinussatz, Winkelsumme) kannst du die drei Winkel und damit jeweils die Fläche des zugehörigen Kreisausschnitts (innerhalb des Dreiecks) ausrechnen:

w1 ≈ 33,56°  , w2 ≈  84,26°  ,  w3 ≈ 62,18°

Fläche des  Kreisausschnitts zu w1 = w1 * π * r₁² / 360°

       die beiden anderen KA analog

Fläche ΔABC  =  1/2 * AB * AC * sin(w1)

Eingeschlossene Fläche = Dreieck - 3 Kreisausschnitte

Gruß Wolfgang

Comments

Vielen lieben Dank für das Nachrechnen und dem Erklären. Das hat mir sehr geholfen

Answer 2

ich weiß, dass es eine Formel gibt

Das ist schon ein sehr fragwürdiger Ansatz, weil die Suche nach einer "fertigen" Formel kontraproduktiv ist und kaum etwas mit Erkenntnisgewinn zu tun hat.

Wenn du die drei Kreismittelpunkte verbindest, erhältst du ein Dreieck.

ich weiß, dass ... man Werte voneinander abziehen muss.

Das ist immerhin schon etwas. Wenn man von dieser Dreiecksfläche die Fläche der drei entstehenden Kreissektoren subtrahiert, erhält man die Größe die Fläche zwischen den drei Kreisen.

Die Fläche eines Kreissektors wird übrigens vom Radius und von der Größe des aufgespannten Zentriwinkels bestimmt. Kommst du damit etwas weiter?

Comments

Dass die 3 Kreise eine Dreiecksfläche bilden, habe ich auch schon daran gedacht. Allerdings habe ich mit Kreissektoren bisher noch nie gerechnet. Jetzt weiß ich, wie ich vorgehen kann. Danke für Ihre Hilfe!