Aufgabe:
Diese Funktion beschreibt die Außentemperatur:
Ti(t)= 8 . sin (pi/12 (t-10,5)) +20
Diese Funktion beschreibt die Temperatur in einem Nest (Innentemptratur):
TA(t)= 3 . sin (pi/12 (t-11,5)) +32
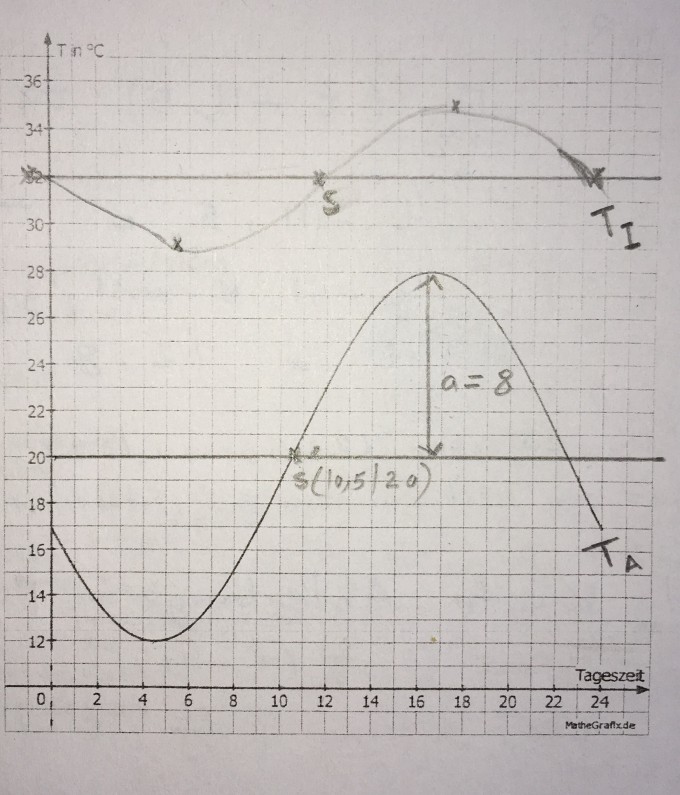
Wie man merkt, (von Maxima und Minima in den Grafen), es gibt eine zeitliche Verzögerung von einer Stunde im Nest (logisch).
Problem/Ansatz:
Untersuchen Sie, bei welcher Außentemperatur die Temperaturabnahme im Nest maximal ist.
Alles was der damalige Lehrer sagte "Es handelt sich um die zweite Ableitung ".
Ich werde also die zweite Ableitung von Außentemperatur-Funktion berechnet und dann gleich null setzen und dann durch Vorzeichentabelle Wendepunkt bestimmen, und dann eine Stunden addieren zu dem x-wert des Wendepunkt (da Temperatur innen eine Stunde später außen entspricht ). Stimmt das?
Also ich leite ab:
TA'(t)= 8 . cos (pi/12(t-10,5)) . pi/12.1
= 2/3 pi . cos (pi/12 (t-10,5)
TA'' = 2/3 pi . -sin (pi/12 (t-10,5) . pi/12 .1
= -pi^2 / 18 sin (pi/12 (t-10,5)
doch jetzt weiß ich nicht, wie es weitergeht, wie soll ich das gleich null setzen und dann Vorzeichentabelle erstellen?
Und eine andere Frage, kann man nicht die Wendepunkte dem Grafen entnehmen? (Bild hochgeladen)