Aufgabe:
Eine Leuchtreklame wird mit zahlreichen Glühbirnen beleuchtet, von denen fast täglich welche ausfallen.
Wenn mehr als 5 Glühbirnen ausfallen, lässt der Betreiber der Leuchtreklame die Birnen ersetzen. An
30 aufeinander folgenden Tagen wurde gezählt, wie viele Birnen pro Tag ausgefallen sind. Dies lieferte folgende Häufigkeitstabelle.
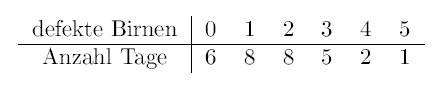
a) Bestimmen Sie den Parameter der Poisson-Verteilung so, dass E(X) mit dem arithmetischen Mittel
der beobachteten Ausfälle übereinstimmt.
b) Vergleichen Sie die gemessenen relativen Häufigkeiten mit den entsprechenden Wahrscheinlichkeiten
der Poisson-Verteilung.
c) Wir groß ist die Wahrscheinlichkeit, dass an einem Tag genug Birnen ausfallen, um eine Auswechslung
vorzunehmen?
Problem/Ansatz:
Aufgabe a) habe ich bereits gelöst.
Bei Aufgabe b), habe ich bereits folgendes:
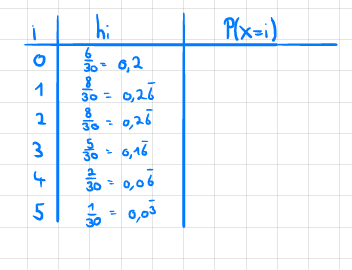
Für die Poission verwende ich folgende Formel:
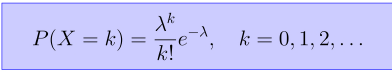
K = 0,1,...etc. Was setze ich für Lamda ein?
Es wäre sehr nett, wenn mir jemand sagen könnte, was ich für die Formel einsetzten muss. Vielen Dank im Voraus.
Euer Max