Stapel von n Brettern, so dass er gerade nicht umfällt...

Question

Aufgabe:

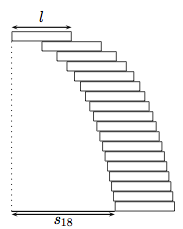
Wie weit kann ein Stapel \( n \) gleich grosser Bretter der Länge \( l \) maximal überragen, ohne dass er umkippt? Was geschieht für \( n \rightarrow \infty ? \) \( \frac{!}{!}{1} \)

Hinweis: Man berechne rekursiv die grösstmögliche Verschiebung \( s_{k} \) des \( k \) -ten gegen das oberste Brett.

Nun frage ich mich:

- ist k die Anzahl der Bretterlängen, l , welche das meist verschobene Brett das Fundamentbrett überragt?

- muss man hier nicht noch irgendwie etwas über die Physik so eines Stapels wissen?

- die Erfahrung zeigt, dass man den hier angegebene Stapel so stabilisieren könnte:

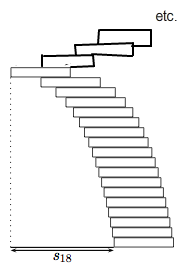
sollte ich dies auch in Betracht ziehen.

Also generell gesagt: Was ist genau die Bedingung die den Stapel zum umfallen bringt?

Comments

eine Lösung für dich habe ich nicht aber zum besseren Verständnis :

  - der Schwerpunkt eines Brettes ( Mitte Länge ) muß sich noch innerhalb der Länge
des darunterliegenden Brettes befinden.

  - der Gesamtschwerpunkt des Stapels muß sich noch innerhalb der Länge des zu
unterst liegenden Brettes befinden.

  mfg Georg

Answer 1

Schau mal folgendes Video an:

ab 6. Minute. Dort wird diese Reihe etwas untersucht.

Comments

Danke für eure Antworten.

Ich verstehe, dass man die Distanz sich so vorstellen kann:

1/2 + 1/4 + 1/6 + ....  = ∑ 1/2n = 1/2 * ∑ 1/n  (mit n=Anzahl Bretter)

Und das der lim von der harmonischen Reihe nach unendlich strebt (haben wir in der VL auch schon bewiesen...)


Ich weiss nun aber nicht wie ich das rekursiv beweisen kann...


Lg

Tulbih

---

Du willst beweisen das Die Reihe gegen unendlich geht ?

Das hatte man doch im Video recht gut erklärt.

---

Ich glaube ja, dass ich mit

\( \lim \limits_{n \rightarrow \infty} \sum \limits_{k=1}^{n} \frac{1}{2 k}=\frac{1}{2} \lim \limits_{n \rightarrow \infty} \sum \limits_{k=1}^{n} \frac{1}{k}=\ldots \) harmonische Reihe...\( =\frac{1}{2} \infty=\infty \)

die Aufgabenstellung eventuell schon beantwortet habe, bin mir aber nicht sicher.

---

Doch. Das wäre auch ein gültiger Beweis. Notfalls kann man die harmonische Reihe ebenso wie im Video zeigen über das zusammenfassen von Summanden.