.. das ist jetzt meine Antwort:
Ich habe nur gleichseitige Dreiecke mit ganzzahlen Eckkoordinaten gefunden, die senkrecht auf einer der vier Raumdiagonalen stehen. Das bedeutet für ihre Generierung:
1.) Nehme einen beliebigen Punkt - z.B.) $$\vec{a} = \begin{pmatrix} 1 \\ 2 \\ 3\end{pmatrix}$$2.) Suche Dir eine der vier Raumdiagonale aus - z.B. \(d_4=\begin{pmatrix} 1 \\ -1 \\ 1\end{pmatrix}\) . Die zugehörige Rotationsmatrix ist $$D_4 = \begin{pmatrix} 0& -1& 0\\ 0& 0& -1\\ 1& 0& 0 \end{pmatrix}$$3.) rotiere \(\vec{a}\) zweimal um die Raumdiagonale um den Winkel von jeweils \(120°\):$$\begin{aligned} \vec{b} &= D_4 \cdot \vec{a} &&= \begin{pmatrix} 0& -1& 0\\ 0& 0& -1\\ 1& 0& 0 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 2 \\ 3\end{pmatrix} &= \begin{pmatrix} -2 \\ -3 \\ 1\end{pmatrix}\\ \vec{c} &= D_4 \cdot \vec{b} &&= \begin{pmatrix} 0& -1& 0\\ 0& 0& -1\\ 1& 0& 0 \end{pmatrix} \cdot \begin{pmatrix} -2 \\ -3 \\ 1\end{pmatrix} &= \begin{pmatrix} 3 \\ -1 \\ -2\end{pmatrix}\end{aligned}$$Anschließend kann man das Dreieck noch beliebig verschieben, indem man alle drei Punkte mit einem gemeinsamen Offset \(\begin{pmatrix} x & y& z\end{pmatrix}^T\) addiert.
Die anderen drei Rotationsmatrizen sind:$$\begin{aligned} D_1 &= \begin{pmatrix} 0& 0& 1\\ 1& 0& 0\\ 0& 1& 0 \end{pmatrix}\\ D_2 &= \begin{pmatrix} 0& -1& 0\\ 0& 0& 1\\ -1& 0& 0 \end{pmatrix}\\ D_3 &= \begin{pmatrix} 0& 0& -1\\ 1& 0& 0\\ 0& -1& 0 \end{pmatrix}\end{aligned}$$Diese Roationen sind jeweils zyklische Vertauschungen der Koordinaten. Damit ist zum einen die Ganzzahligkeit der Koordinaten garantiert. Weiter hat jede der Rotationsmatrizen die Eigenschaft, dass \(D_i^3 = E\) ist (\(E\) ist die Einheitsmatrix). Damit führt jede eine Drehung um jeweils \(120°\) durch, was dann zu dem gleichseitigen Dreieck führt.
In folgendem Bild kann man das Ergebnis für das Beispiel oben (das grüne Dreieck) und für den Punkt \(A=\begin{pmatrix} 2& 1& 0\end{pmatrix}^T\) gedreht mit \(D_1\) sehen (das blaue Dreieck) inklusive einer Verschiebung um 3 Einheiten in Richtung \(z\).
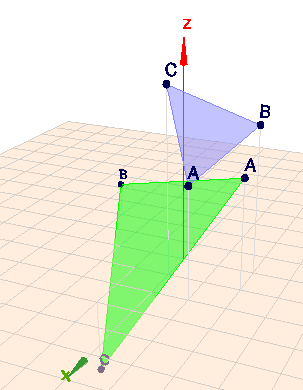
(klick auf das Bild, dann kann man die Szene rotieren)
Der von Dir vorgeschlagen Weg ist eine Teilmenge dieser Lösung. Bei Dir ist immer \(\vec{a} = \begin{pmatrix} 0& b& a \end{pmatrix}^T\) und die Rotationsmatrix ist \(D_1\).
Wie ich finde, eine ziemlich interessante Frage. ich suche noch nach anderen Möglichkeiten für solche Dreiecke oder einem Beweis, dass es keine andere Möglichkeit mehr gibt ... ;-)
Falls Du noch Fragen hast, so melde Dich bitte.
Gruß Werner
.. und das war mal ein Kommentar:
Ich unterstelle, dass \(\vec{a}\), \(\vec{b}\) und \(\vec{c}\) die Koordinaten der Eckpunkte sein sollen. Dann ist $$\vec{b} - \vec{a} = \begin{pmatrix} a\\ -b\\ b-a\end{pmatrix} \ne \begin{pmatrix} a\\ b\\ a-b \end{pmatrix}$$
und wenn die Seiten nur aus zyklisch vertauschten Koordinaten bestehen, so ist das Dreieck immer gleichseitig und nicht nur gleichschenklig.
Sollen nur die Koordinaten ganzzahlig sein oder auch die Seitenlängen?