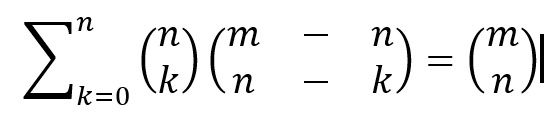
Welche Bedeutung hat jeder Term?
Binomialkoeffizient rechts: Anzahl aller n-elementigen Teilmengen einer Menge mit m Elementen.
1. Binomialkoeffizient links: Anzahl aller k-elementigen Teilmengen einer Menge mit n Elementen.
2. Binomialkoeffizient links: Anzahl aller k-n -elementigen Teilmengen einer Menge mit m-n Elementen.
Summenzeichen: k läuft von 0 bis n.
Daraus ergibt sich ein Beweis der obigen Summenformel ohne Rechnung.
[spoiler]
Unterteile die gegebene Menge mit m Elementen in zwei Teilmengen. Eine mit n Elementen T1, die andere mit den übrigen n-m Elementen T2.
Wenn du nun n-elementigen Teilmengen der gesamten Menge mit m Elementen betrachtest, können ihre Element aus den beiden Teilmengen stammen.
Man wählt einige Elemente aus T1 und die andern aus T2. Innerhalb von T1 und T2 kann man unabhängig voneinander die richtige Anzahl Elemente auswählen und hat so die Anzahl der n-elementigen Teilmengen der Gesamtmenge auf m Elementen bestimmt. Fertig.
Konkret zählst du nun links zusammen:
(Die Zahl der Teilmengen aus T1 mit 0 Elementen )*(Zahl der Teilmengen aus T2 mit n Elementen)
+
(Die Zahl der Teilmengen aus T1 mit 1 Element )*(Zahl der Teilmengen aus T2 mit n-1 Elementen)
+
(Die Zahl der Teilmengen aus T1 mit 2 Elementen )*(Zahl der Teilmengen aus T2 mit n-2 Elementen)
usw.
+
(Die Zahl der Teilmengen aus T1 mit n Elementen )*(Zahl der Teilmengen aus T2 mit 0 Elementen)
=
Zahl der Teilmengen aus der Gesamtmenge mit n Elementen