c ist ein Element der Reellen Zahlen. Gleichung lösen

Question

Wie kann man dieses Gleichungssystem lösen ohne Zahlen?

a₁ < a₂ < .... < a_n

Die Gleichung

\( \frac{1}{x-a_{1}}+\frac{1}{x-a_{2}}+\ldots+\frac{1}{x-a_{n}}=c(c \in \) reelle Zahlen \( ) \)

hat im Fall c = 0 genau n-1 reelle Lösungen, im Fall c ungleich 0 genau n.

Answer 1

Hier eine Skizze des Lösungswegs:

a1≠0, a2≠0 , ...

Hauptnenner ist hier (x-a1)(x-a2)......(x-an)

Wenn nun die Gleichung mit dem HN mult. wird, resultiert im Fall a)

Links von Gleichheitszeichen Ein Polynom vom Grad n-1. Das hat maximal n-1 Nullstellen.

im Fall b)

ergibt sich rechts ein Polynom vom Grad n, links vom Grad n-1. So was kann man umformen auf 0 = Polynom vom Grad n. Daher maximal n Nullstellen.

Comments

Wenn nun die Gleichung mit dem HN mult. wird, resultiert im Fall a) Links von Gleichheitszeichen Ein Polynom vom Grad n-1. Warum? Links erhält man doch eine Summe von Zählern, bei denen zwar jeder Zähler separat betrachtet ein Polynom vom Grad n-1 ist, aber als Summe gesehen kommt man doch wieder auf Grad n.

---

Ganz links kannst du ja der ersten Summanden mit  (x-a1) kürzen.

Es bleibt nur

(x-a2)......(x-an)

D.h. ein Term vom Grad n-1.

Das gilt analog für jeden Summanden auf der linken Seite.

---

Das erklärt aber nicht, warum die Gleichung genau  n, bzw.  n - 1  reelle Nullstellen hat.

---

Ja. Das habe ich auch nicht behauptet. Ich hab dir mal das bewiesen, was ich geschrieben hatte. Jetzt musst du noch berücksichtigen, dass die a1, a2, … alle verschieden sind. Vielleicht bringt dich das noch etwas weiter.

Answer 2

Definiere  f : ℝ \ { a₁,...,a_n} → ℝ  durch$$f(x)=\frac1{x-a_1}+\cdots+\frac1{x-a_n}+c$$Betrachte die Teilintervalle
J₀ = (-∞,a₁), J_k = (a_k,a_k+1)  für  k = 1,...,n-1  und  J_n = (a_n,+∞).
In  J₀  gilt  f(x) → c  für  x → -∞  und  f(x) → -∞  für  x → a₁.
In  J_k  gilt  f(x) → +∞  für  x → a_k  und  f(x) → -∞  für  x → a_k+1  und  k = 1,...,n-1.
In  J_n  gilt  f(x) → +∞  für  x → a_n  und  f(x) → c  für  x → +∞.
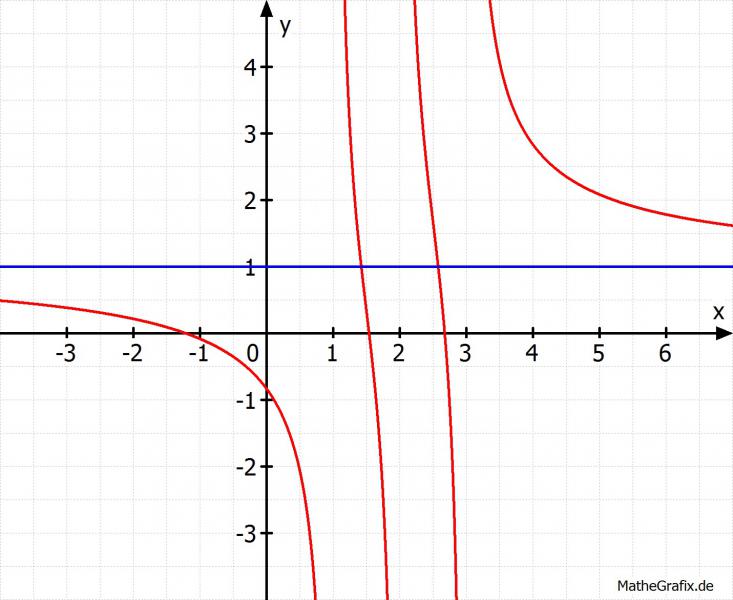
Auf jedem Teilintervall ist  f  differenzierbar. Wegen  f'(x) < 0  für alle  x ∈ ℝ \ { a₁,...,a_n}  ist  f  streng monoton fallend auf jedem der Teilintervalle. Daher existiert in jedem Teilintervall  J_k  für  k = 1,...,n-1  genau eine Nullstelle. Ist  c = 0, existieren keine weiteren Nullstellen. Ist  c > 0, existiert genau eine weitere Nullstelle  in  J₀. Ist  c < 0, existiert genau eine weitere Nullstelle in  J_n. Zur Veranschaulichung sei die Beispielfunktion mit  n = 3, a₁ = 1, a₂ = 2, a₃ = 3  und c = 1  in folgender Skizze dargestellt.