Das, was man Stammfunktion nennt, ist erstmal ein unbestimmtes Integral, da du noch keine Grenzen festgelegt hast.
Die Idee, die dahinter steckt ist folgende. Du hast eine Kurve gegeben und willst unter ihr die Fläche auf einem Intervall wissen. Das will man nun mit ganz einfachen Mitteln ausrechnen. Man unterteilt das ganze in n Rechtecke. Lässt man n unendlich groß werden, so wird die Unterteilung auch immer feiner, sodass man die gesamte Fläche unter der Kurve bekommt. Betrachte mal die Funktion $$ f(x)=x $$ auf dem Intervall [0;t].
Mich interessiert die Fläche unter f auf meinem Intervall.
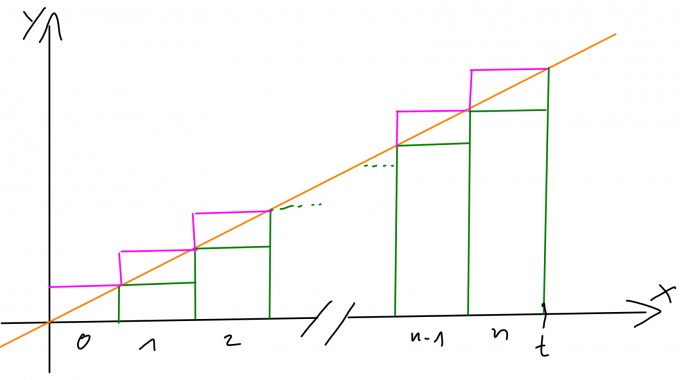
Die grünen Rechtecke sind unterhalb von f und die rosanenj oberhalb von f. Ich bilde also eine Ober - bzw. Untersumme aller Flächeninhalte der jeweils grünen bzw. rosanen Rechtecke. Die haben die Breite t/n.
Untersumme: $$ U_n=\frac{t}{n}\cdot f\Big(\frac{0\cdot t}{n}\Big)+\frac{t}{n}\cdot f\Big(\frac{1\cdot t}{n}\Big)+...+\frac{t}{n}\cdot f\Big(\frac{(n-1)\cdot t}{n}\Big) \\=\frac{t}{n} \cdot \Big(f\Big(\frac{0\cdot t}{n} \Big)+f\Big(\frac{1\cdot t}{n}\Big)+...+f\Big(\frac{(n-1)\cdot t}{n}\Big)\Big)\\=\frac{t}{n}\cdot \Big(0+\frac{t}{n}+...+\frac{(n-1)\cdot t}{n} \Big)\\=\frac{t}{n}\cdot \frac{t}{n}\cdot \Big(0+1+...+(n-1) \Big)\\\stackrel{(*)}{=}\frac{t^2}{n^2}\cdot \frac{n(n-1)}{2}=\frac{t^2}{2}\cdot \frac{n^2-n}{n^2}$$
Obersumme: $$ U_n=\frac{t}{n}\cdot f\Big(\frac{1\cdot t}{n}\Big)+\frac{t}{n}\cdot f\Big(\frac{2\cdot t}{n}\Big)+...+\frac{t}{n}\cdot f\Big(\frac{n\cdot t}{n}\Big) \\=\frac{t}{n} \cdot \Big(f\Big(\frac{1\cdot t}{n} \Big)+f\Big(\frac{2\cdot t}{n}\Big)+...+f\Big(\frac{n\cdot t}{n}\Big)\Big)\\=\frac{t}{n}\cdot \Big(\frac{t}{n}+\frac{2\cdot t}{n}+...+\frac{n\cdot t}{n} \Big)\\=\frac{t}{n}\cdot \frac{t}{n}\cdot \Big(1+2+...+n \Big)\\\stackrel{(*)}{=}\frac{t^2}{n^2}\cdot \frac{n(n+1)}{2}=\frac{t^2}{2}\cdot \frac{n^2+n}{n^2}$$
(*) Gaußsche Summenformel: $$ 1+...+m=\frac{m(m+1)}{2} $$
Die tatsächliche Fläche befindet sich also zwischen der Unter -und der Obersumme.
Lasse ich nun n gegen Unendlich laufen, habe ich eine Summe bekommen, die aus unendlich vielen Rechtecken besteht:
$$ \lim_{n \to \infty} U_n= \lim_{n \to \infty} \frac{t^2}{2}\cdot \frac{n^2-n}{n^2}=\frac{t^2}{2}$$
$$ \lim_{n \to \infty} O_n= \lim_{n \to \infty} \frac{t^2}{2}\cdot \frac{n^2+n}{n^2}=\frac{t^2}{2} $$
Also lautet hier das bestimmte Integral $$ \int_0^t x \ dx=\frac{t^2}{2} $$
Sind die Grenzen nicht bekannt, so heißt es unbestimmtes Integral und man schreibt einfach $$\int x \ dx = \frac{x^2}{2}+C=:F_C(x)$$, die Stammfunktion, die somit für die Flächenberechnung wichtig ist.