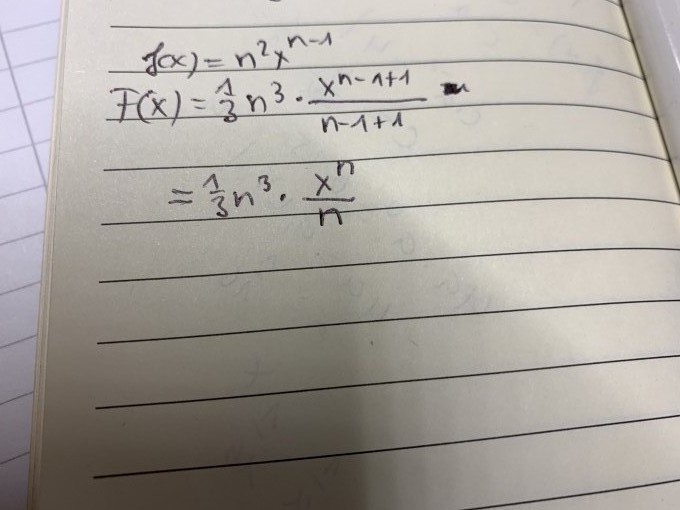Aufgabe: Stammfunktion von
f(x)= n^2• xn-1
Problem/Ansatz:
Prinzipiell habe ich verstanden wie man die Stammfunktion bildet, aber die ^n-1 verwirren mich.
Meine Lösung : F(x)= 1/3 n^3 • x^n/n
Ich bin mir nur unsicher und würde mich freuen, wenn jemand mit Ahnung mal schauen könnte, ob es auch richtig ist oder nicht. Vielen Dank im voraus!