Durch f wird eine Ellipse beschrieben, es entsteht bei der Rotation ein Ellipsoid.
Bei g liegt eine Hyperbel vor. Bei der Rotation entsteht ein Hyperboloid, dessen Volumen unendlich groß ist. Falls bei g ein Tippfehler vorliegt und ein + statt - stehen sollte, handelt es sich auch um eine Ellipse bzw. ein Ellipsoid.
Berechnet wird das Volumen mit folgender Formel.
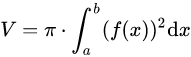
Die Grenzen sind jeweils die von dir angegebenen Nullstellen der Funktionen.