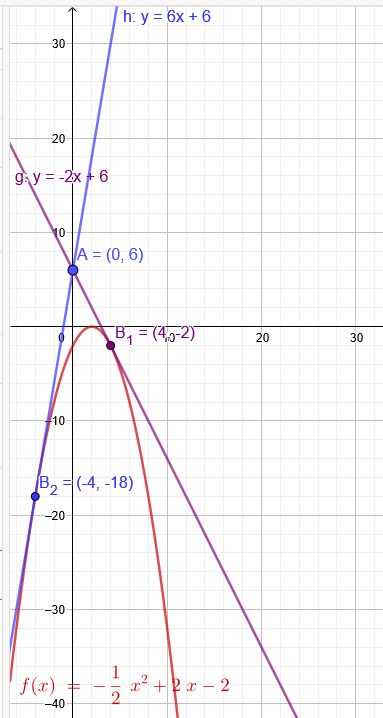
\(f(x)=-0,5x^2+2x-2 \) \(A(0|6)\) \(f´(x)=-x+2\)
Berührpunkte sind:
\(B(x|-0,5x^2+2x-2\)
\( \frac{-0,5x^2+2x-2-6}{x-0}=-x+2 \) → \( \frac{-0,5x^2+2x-8}{x}=-x+2 \)
\( -0,5x^2+2x-8=-x^2+2x \)
\( 0,5x^2-8=0\)
\( x_1=4\) \(f(4)=-2 \) \(f´(4)=-2\)
\( x_2=-4\) \(f(-4)=-8-8-2=-18 \) \(f´(-4)=6\)
Nun noch die Tangenten aufstellen.