Bei einem Trapez \(ABCD\) (grün) seien die Seiten \(AB=a\) und \(CD=c\) parallel. Führe bei diesem Trapez am Mittelpunkt \(Z\) der Seite \(BC\) eine Punktspiegelung durch. Das Originaltrapez und das gespiegelte Trapez \(A'CBD'\) bilden zusammen das Parallelogramm \(AD'A'D\).
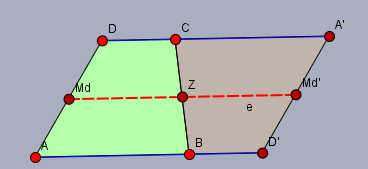
Bei einem Parallelogramm schneiden die Seiten aus einer Gerade, die parallel zum anderen Seitenpaar verläuft, ein Stück heraus, was genauso lang ist, wie eine dazu parallele Seite. In diesem Fall ist also \(|M_dM_d'| = |AD'| = a+c\). Und wegen der Punktspiegelung ist \(|M_dZ|=|ZM_d'|=m\). D.h. Der Punkt \(Z\) halbiert die Strecke \(|M_dM_d'|\). Folglich ist$$m = \frac 12 |M_dM_d'| = \frac 12 (a+c)$$ Gruß Werner