Dieses Video zum Satz des Pythagoras hatte ich vor einigen Jahren entwickelt und mich jetzt entschieden, es auf Youtube zu veröffentlichen, da der Inhalt einfach wichtig ist und in jedes Lehrbuch gehört.
Mich hatte immer gestört, dass man nicht erkennen kann, dass bei der Standarddarstellung:
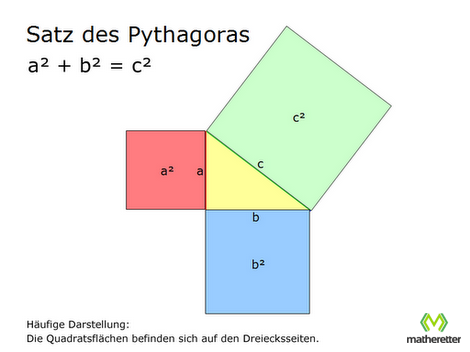
die kleinen Quadratsflächen zusammen die große Quadratsfläche ergeben.
Nach dem Durchforsten mehrerer Skripte, bin ich damals glücklicherweise auf einen Ähnlichkeits-Hinweis in einem Skript gestoßen, der mir die Augen öffnete. Das war ein sehr schöner Moment, denn das „Warum“ ist so wunderschön einfach zu verstehen - und mit den Visualisierungen konnte ich es sehr einfach darstellen.
„Die Quadratsflächen sind die vergrößerten Dreiecksflächen, deren Form verändert wurde, doch deren Flächeninhalt gleich bleib. Daher: A+B = C. Beide Teildreiecke A und B müssen das Gesamtdreieck C ergeben. Also müssen auch ihre Flächenvergrößerungen m·A + m·B = m·C (in Dreiecksform oder Quadratsform dargestellt) zusammengehören.“
Im Wiki: Prinzip hinter dem Satz des Pythagoras
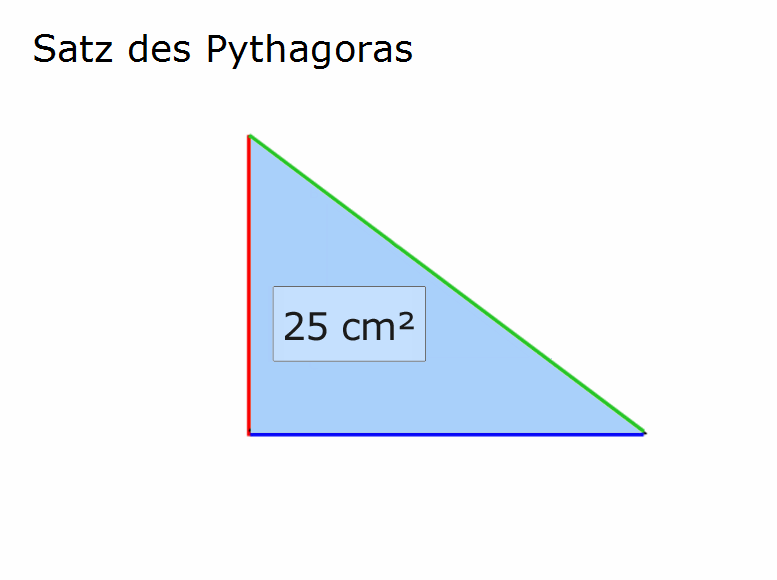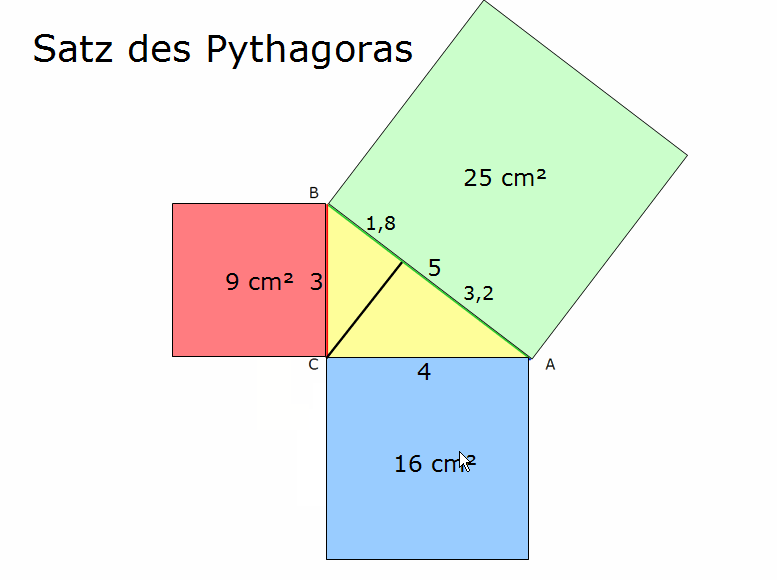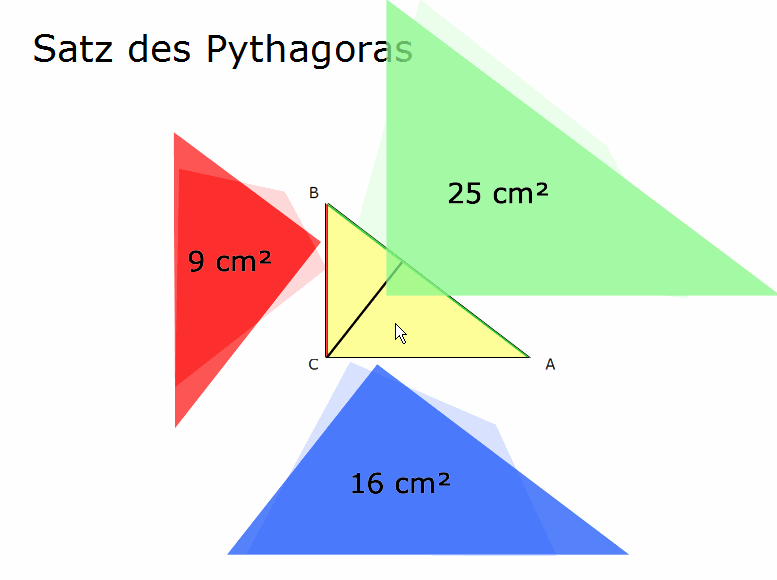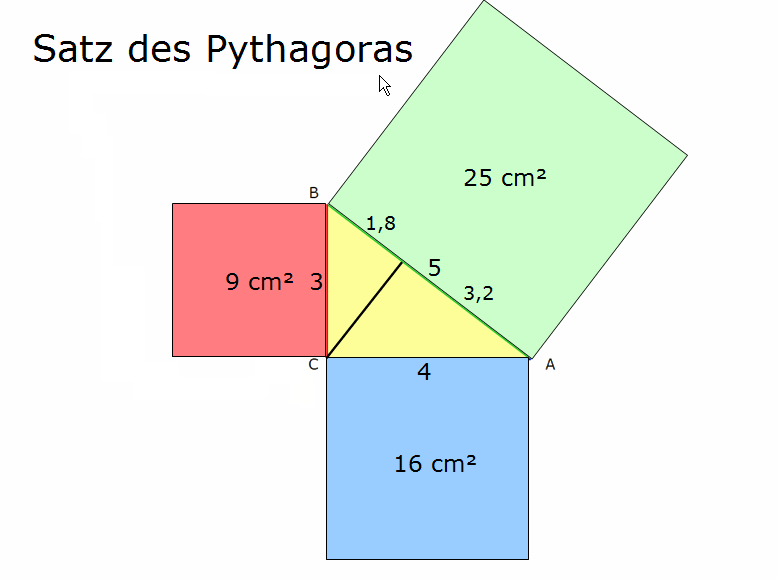
Formell wird das Prinzip oben übrigens so ausgedrückt:
Ea = m·a², Eb = m·b², Ec = m·c²,
wobei Ea + Eb = Ec und damit auch m·a² + m·b² = m·c² → a² + b² = c²
"E" meint dabei die jeweilige Dreiecksfläche und "m" den Vergrößerungsfaktor, der für alle Flächen gilt.