Die Quadrate ABCD und BEFG seien so angeordnet, dass BG auf BC liegt und E sowie F außerhalb ABCD liegen (siehe Abbildung). Im Inneren des Sechsecks AEFGCD liegt an beliebiger Stelle ein Punkt P.
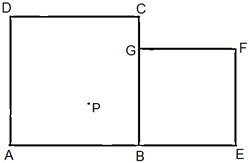
Der Vektor \( \vec{AG} \) bildet P auf P‘ ab, der Vektor \( \vec{EC} \) bildet P‘ auf P‘‘ ab und der Vektor \( \vec{GA} \) bildet P‘‘ auf P‘‘‘ ab. Zeige, dass die Quadrate ABCD und BEFG zusammen die gleich Flächengröße haben, wie das Quadrat PP’P‘‘P‘‘‘. Wie viele Beweise des Satzes von Pythagoras ergeben sich auf diese Weise?