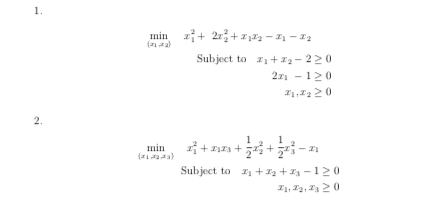
1.)$$\begin{aligned} \substack{ \min \\ (x_1,x_2)} \quad x_1^2 + 2x_2^2 +x_1x_2 -x_1 - x_2 \\ \text{Subject to} \quad x_1 + x_2 - 2 &\ge 0 \\ 2x_1-1 &\ge 0\\ x_1, x_2 &\ge 0 \end{aligned}$$ 2.) $$\begin{aligned} \substack{ \min \\ (x_1,x_2,x_3)} \quad x_1^2 + x_1x_3 + \frac 12 x_2^2 + \frac 12 x_3^2 - x_1 \\ \text{Subject to} \quad x_1 + x_2 +x_3 - 1 &\ge 0\\ x_1, x_2,x_3 &\ge 0 \end{aligned}$$
Aufgabe:
Erstelle ein linear complementarity problem und löse quadratic programming problem