Aufgabe:
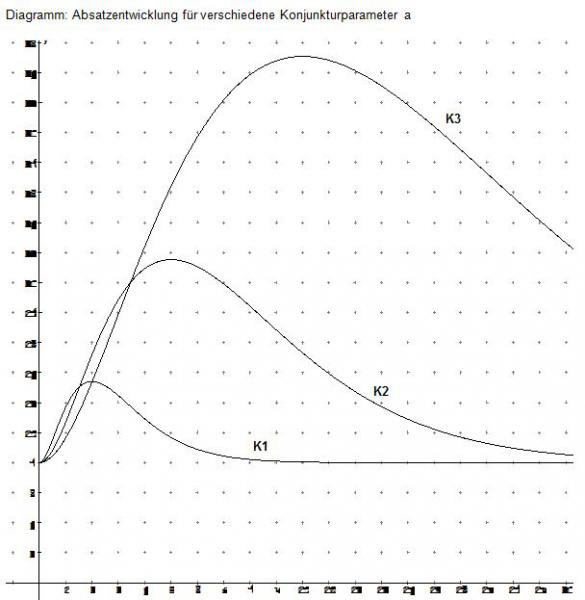
Die Absatzentwicklung eines Unternehmens soll in Abhängigkeit von einem Konjunkturparameter a mit Hilfe der Funktion Na untersucht werden (vgl. Anlage: Diagramm mit Beispiel-Absatzkurven).
\( N_{a}(t)=8+\frac{10 a t^{2}}{e^{a t}} \quad \) mit \( t \in(0 ; 20] ; \) Parameter \( \mathrm{a}>0 \)
Einheiten: \( \mathrm{t} \) Zeit in Monaten; \( \mathrm{N}_{\mathrm{a}} \) (t) Abs atz in ME pro Monat [1000 Stck/Monat]
mit ; Parameter a > 0
Einheiten: t Zeit in Monaten; Na(t) Absatz in ME pro Monat [1000 Stck/Monat]
Hinweis: Es gilt:
\( N_{a}^{\prime}(t)=\frac{10 a t \cdot(a t-2)}{e^{a t}} \quad N_{a}^{\prime \prime}(t)=\frac{10 a \cdot\left(2-4 a t+a^{2} t^{2}\right)}{e^{a t}} \)
a. Untersuchungen für den Parameterwert a = 0,5:
I. Skizzieren Sie den Graphen von mit Hilfe einer Wertetabelle
im beigefügten Diagramm.
II. Bestimmen Sie den Zeitpunkt t mit maximalem Absatz.
III. Untersuchen Sie, zu welchem Zeitpunkt die Absatzrate maximal wird (nur notwendige Bindung ausführen).
b. Allgemeine Untersuchungen mit dem Parameter a:
I. Zeigen Sie durch schrittweise Berechnung, wie man die oben gegebenen Ableitungsterme von und bestimmt hat.
II. Ermitteln Sie für die Funktionenschar mit Hilfe einer hinreichenden Bedingung die Zeitpunkte t mit maximalem Absatz (abhängig vom Parameter a).
III. Weisen Sie nach, dass alle HP der Kurvenschar auf einer Geraden liegen (Ortskurve)!
c. Bestimmen Sie zu den im Diagramm dargestellten Absatzkurven K1, K2 und K3 die zugehörigen Parameterwerte a.