Wie löst man die Gleichung nach x hin auf? 0 = 2x + ln(2x+1) * (2x-1)

Question

Wie löst man diese Gleichung nach x hin auf?

\( O=2 x+\ln (2 x-1) *(2 x-1) \)

Answer 1

Hi,

das kann man algebraisch nicht lösen. Da bräuchte es ein Näherungsverfahren.

https://www.mathelounge.de/49035/mathe-artikel-das-newtonverfahren

Newton wäre hier eine geeignete Wahl.


Allerdings gibt es hier gar keine Nullstellen ;).

(Wenn gefordert könnte man das sogar zeigen)


Grüße

Comments

Könnte man dann nicht theoretisch auch mit einen graphikfähigen Taschenrechner die Schnittpunkt(e) von zwei Graphen ablesen? (Hier gäbe es dann dementsprechend natürlich keine)

Wären die zwei Funktionen richtig, um sie jeweils ins Koordinatensystem einzeichnen zu lassen zur Schnittpunktbestimmung?

\( y=2 x \) und \( y=\ln (2 x-1) *(2 x-1) \)

---

Eins von beiden müsste negativ sein ;).

Du hast ja f(x) = g(x), wobei wir f(x) = -2x nehmen.

Dann kann man das nach obigen umformen, bzw. im Schaubild erkennen, dass es keine Schnittpunkte gibt. Genau ;).

Answer 2

Auch wenn die Frage schon alt ist und "Beste Antwort" schon vergeben wurde, kann ich den Satz "...gar keine Nullstellen" nicht so ... stehen sehen.  

Es gibt schon über 200 Jahre komplexe Zahlen und die Umkehrfunktion zu x * e^x : LambertW(x)  

0=2x+log(2x-1)*(2x-1) | -1

-1=(2x-1)+log(2x-1)*(2x-1) | subst1: u=2x-1 und Exponentialfunktion

exp((-1-u)/u)=u  |*(-1/u)

e^{-1/u-1} *(-1/u)=-1

e^{-1/u} *(-1/u)=-e  |subst2: z=-1/u und Umkehrfunktion

z=LambertW(-e)  | Rücksubst2:

u=-1/LambertW(-e) | Rücksubst1:

2x-1=-1/LambertW(-e)

x=(1-1/LambertW(-e))/2  

Gute Rechner können das berechnen:http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php 

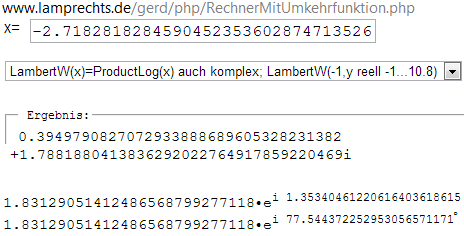
also

x1= 0.44111161967499482446076447024089.. +0.26660525097138465444099823482124... i  

LambertW hat auch 2 Lösungen: W(-1,-e) also 2. komplexe Lösung: 

x2= 0.44111161967499482446076447024089.. -0.26660525097138465444099823482124... i  

Comments

Wenn jedoch die Formel der Überschrift gemeint sein soll (also +1 statt -1):  

0=2x+log(2x+1)*(2x-1)  

2x = log(2x+1)*...

dann sieht man sofort die Lösung bei x=0 denn 

2*0 = log(1)*...