Aufgabe:
Begründung der Abstandsformel:
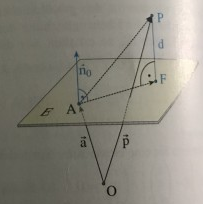
P sei ein Punkt, der auf derjenigen Seite der Ebene E liegt, nach der \( \vec{n}_{0} \) zeigt. Dann gilt folgende Rechnung:
\( (\vec{p}-\vec{a}) \cdot \vec{n}_{0}=\overrightarrow{A P} \cdot \vec{n}_{0}=(\overrightarrow{A F}+\overrightarrow{F P}) \cdot \vec{n}_{0} \)
\( =\overrightarrow{\mathrm{AF}} \cdot \vec{n}_{0}+\overrightarrow{\mathrm{FP}} \) \( =|\overrightarrow{\mathrm{AF}}| \cdot\left|\overrightarrow{\mathrm{n}}_{0}\right| \cdot \cos 90^{\circ}+|\overrightarrow{\mathrm{FP}}| \cdot\left|\overrightarrow{\mathrm{n}}_{0}\right| \cdot \cos 0 ° \) \( =|\overrightarrow{\mathrm{FP}}|= d \)
Liegt P auf der anderen Seite von E, so ergibt sich \( (\vec{p}-\vec{a}) \cdot \vec{n}_{0}=-d \)
Insgesamt: \( d=\left|(\vec{p}-\vec{a}) \cdot \vec{n}_{0}\right| \)
Ansatz:
Ich muss die hessische Abstandsformel herleiten. Ich bräuchte Hilfe woher plötzlich cos 90 Grad bzw. cos 0 Grad herkommen. Der Rest ist soweit eigentlich klar.