Geometrie der komplexen Ebene

Question

Aufgabe: Sei K:={\( \frac{1}{1+it} \)| t∈ℝ}

a) Skizzieren Sie die Menge {\( \frac{1}{1+it} \) | t∈ℤ}

b) Zeigen Sie, dass K auf einem Kreis liegt: K = {x+iy∈ℂ \ {0} | (x-\( \frac{1}{2} \))²+y² = \( \frac{1}{4} \)

Problem: Ich weiß nicht wie ich eine Menge in den komplexen Zahlen Skizzieren kann. Auch die Aufgabe b ist völlig rätselhaft. Ich würde mich sehr über einen Ansatz freuen der mich weiterbringt und über eine Erklärung wie ich denn überhaupt anfange bei dieser Art von Aufgabe.

Answer 1

zunächst 1/1+ik, k∈ℤ

\( \frac{1}{1+ik} \)      erweitern mi 1-ik

= \( \frac{1-ik}{(1+ik)(1-ik)} \)    3. binom.

=  \( \frac{1-ik}{1-(ik)^{2}} \)     i²=-1

=  \( \frac{1-ik}{1+k^{2}} \)       aufspalten in Realanteil + Imaginäranteil

=  \( \frac{1}{1+k^{2}} \) - \( \frac{k}{1+k^{2}} \)*i

Das ergibt den Graph aller dieser Punkte in der Gausschen Ebene, x-Richtung real, y-Richtiung imaginär:

( \( \frac{1}{1+k^{2}} \) I  - \( \frac{k}{1+k^{2}} \) )

zunächst für k∈ℤ:

1 + 0i    Zeichne: (1 I 0)

1/2 ± 1/2 i        Zeichne: (1/2 I ± 1/2 )

1/5 ± 2/5 i        Zeichne: (1/5 I ± 2/5 )

1/10 ± 3/10 i    Zeichne: (1/10 I ± 3/10 )

1/17 ± 4/10 i    Zeichne: (1/17 I ± 4/17 )  usw

jetzt allgemein:

b) Zeigen Sie, dass K auf einem Kreis liegt

heißt: Es ist zu beweisen, nicht abzulesen an einer Zeichnung!

Die Punkte heißen: ( \( \frac{1}{1+t^{2}} \) I  - \( \frac{t}{1+t^{2}} \) )   t∈ℝ

Bilde die Ortskurve, indem du t eliminierst:

x=\( \frac{1}{1+t^{2}} \)

y=  - \( \frac{t}{1+t^{2}} \)

also y=  - x*t, mit t=±\( \sqrt{1/x-1} \)  ergibt sich:

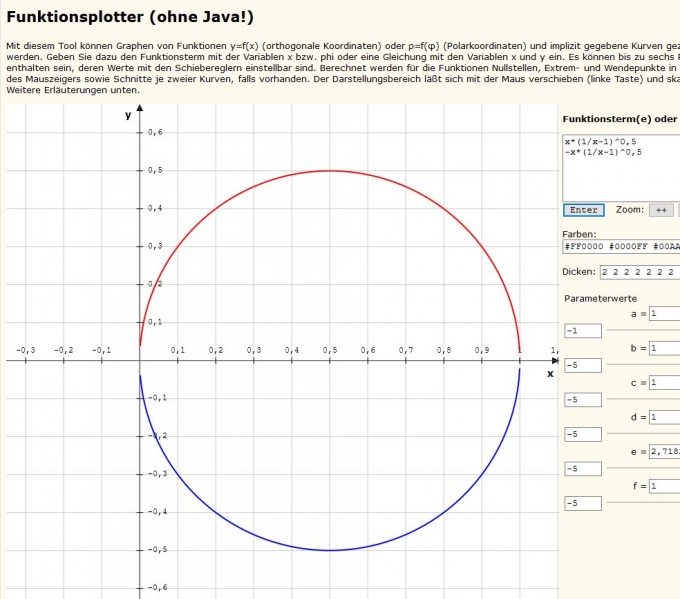
y=  ± x*\( \sqrt{1/x-1} \)    D =]0,1]

y² = x² * (1/x - 1)

y² + x² -x =0

x² -x + 1/4 -1/4 + y² = 0

(x-1/2)² + y² = (1/2)² , D =]0,1]    Kreisgleichung M(0,5 I 0), r=0,5  (0I0) ausgeschlossen!

Bei (1 I 0) rechts ist der Kreis geschlossen (begrenzte Rechenfähigkeit des Plotters)

Answer 2

a) \(\dfrac{1}{1+it}=\dfrac{1-it}{(1+it)(1-it)}=\dfrac{1-it}{1+t^2}=\dfrac{1}{1+t^2}+i\cdot\dfrac{-t}{1+t^2}= x+iy\)

\(x=  \dfrac{1}{1+t^2}~~~; ~~~~y=\dfrac{-t}{1+t^2}\)

t	-3	-2	-1	0	1	2	3	7
x	0.1	0.2	0.5	1	0.5	0.2	0.1	0.02
y	0.3	0.4	0.5	0	-0.5	-0.4	-0.3	-0.14

Offensichtlich liegen die Punkte auf einem Kreis.

b) Kreisgleichung:

\((x-x_M)^2+(y-y_M)^2=r^2\)

Mit M(0.5|0) und r=0.5 erhalten wir \((x-0.5)^2+(y-0)^2=r^2\) bzw. \((x-\frac{1}{2})^2+y^2=\frac{1}{4}\)