a) Der Roboter geht 10 Schritte, 4 nach rechts, 6 nach oben führen zum Ziel.
X=Anzahl der Rechtsschritte, X ist binom.vert. mit n=10, p=0,5
P(X=4) = \( \begin{pmatrix} 10\\4 \end{pmatrix} \) 0,510 = 0,20...
b) Der Roboter geht zunächst 5 Schritte, 2 nach rechts, 3 nach oben führen zum Ziel.
X=Anzahl der Rechtsschritte, X ist binom.vert. mit n=5, p=0,5
P(X=2) = \( \begin{pmatrix} 5\\2 \end{pmatrix} \) 0,55 = 0,31...
Dann geht er von (2|3) nach (4|6), also wieder 5 Schritte, 2 nach rechts, 3 nach oben.
....
P(Aufg,b) = P(X=2) * P(X=2) = 0,097...
c) Fortsetzung von a):
E(X)=n*p=10*0,5=5
d) Der Abstand ist nicht binomialverteilt, man muss den Erwartungswert mühsam ausrechnen:
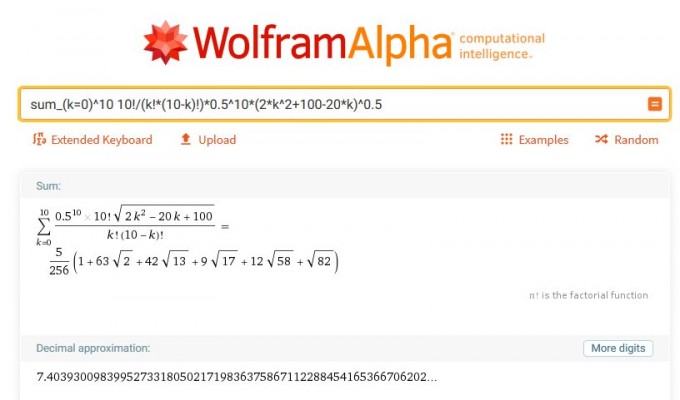
E(Abstand) =\( \sum\limits_{n=0}^{10}{P(X=k)*Abstand(k)} \) = 7,4...
Der Abstand vom Nullpunkt bei k Rechtsschritten ist (k nach rechtes, 10-k nach oben, Pythagoras):
\( \sqrt{k^2+(10-k)^2} \) = \( \sqrt{2*k^2+100-20*k} \)
Kann es sein, dass die Aufg. zu schwer für die Schule ist (oder gehst du in Singapur zur Schule:) und nur gestellt wurde, weil man dachte, die Lösung ginge so:
E(X) = 5, Y=Anzahl der Hochschritte, also E(Y)=5,
also E(Abstand)= \( \sqrt{25+25} \) =7,07...
Das ist nicht der Erwartungswert, sondern der minimale Abstand.
Aufg. 2)
Ein Roboter beginnt im Ursprung eines Koordinatensystems eine Wanderung, bei der er in jede Minute seine Position um eine Einheit in x-Richtung oder in y-Richtung oder in z-Richtung zufällig ändert.
a) Mit welcher Wahrscheinlichkeit ist der Roboter nach 10 Minuten im Punkt P (2|3|5).
X=Schrittzahl in x-Richtung
Y=Schrittzahl in y-Richtung
Z=Schrittzahl in z-Richtung
Der Roboter geht 10 Schritte, 2 in x-Richtung, 3 in y-Richtung, 5 in z-Richtung nach oben führen zum Ziel.
X+Y+Z= n=10, p=1/3
P(X=2,Y=3,Z=5) = \( \begin{pmatrix} 10\\2 \end{pmatrix} \) \( \begin{pmatrix} 8\\3 \end{pmatrix} \) \( \begin{pmatrix} 5\\5 \end{pmatrix} \) (1/3)10 = ..
d.h. Wähle, wo er die 2 geht, wo die 3, wo die 5.
Man kann P umformen, so dass es der Formel für die multinomiale (=polynomiale) Verteilung entspricht:
= \( \frac{10!}{2!8!} \) \( \frac{8!}{3!5!} \) \( \frac{5!}{5!0!} \) (1/3)10
= \( \frac{10!}{2!3!5!} \) (1/3)10
In der Formel stehen die Schrittzahlen einfach im Nenner.
Vgl:
https://www.onlinemathe.de/forum/Erlaeuterung-der-Polynomial-Multinomialverteilung