In der Vorlesung wurde bereits gezeigt:
Seien \((X,\tau_X), (Y,\tau_Y)\) topologische Räume und \(f: X\to Y\) eine Abbildung. Dann ist \(f\) stetig genau dann, wenn:
(a) \(f^{-1}(U)\in \tau_X\) ist für jedes \(U\in \tau_Y\)
Als Merkregel: f ist stetig genau dann, wenn Urbilder offener Mengen offen sind.
Ich soll nun zeigen, dass $$f \text{ ist stetig } \quad \Leftrightarrow \quad \begin{cases}\text{ Für alle bzgl. } \tau _Y \text{ abgeschlossenen } A\subset Y \text{ ist} \\ f^{-1}(A) \text{ abgeschlossen bzgl. } \tau _X\end{cases}$$ Ich habe versucht, die Aussage auf (a) zurückzuführen. Ich möchte also für "\(\Leftarrow\)" zeigen, dass das Urbild von offenen Mengen offen ist bzw. \(f^{-1}(U)\in \tau_X\) für jedes \(U\in \tau_Y\). Hierbei verwende ich den Fakt, dass das Komplement von \(A\subset Y\), also \(Y\backslash A\), offen ist. Selbiges gilt für \(X\backslash f^{-1}(A)\) (auch offen).
Kann ich nun einfach sagen, dass für alle \(y\in Y\backslash A\) gilt, dass \(f^{-1}(y)\in X\backslash f^{-1}(A)\).
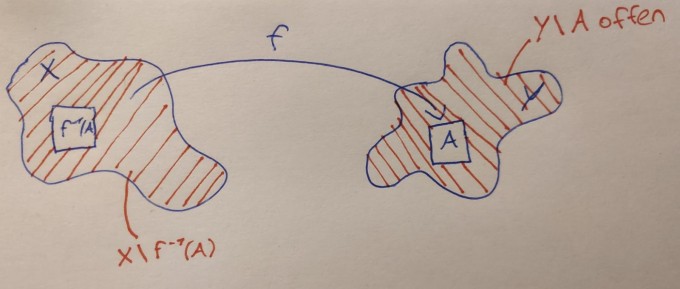
Als Bild: