Aufgabe:
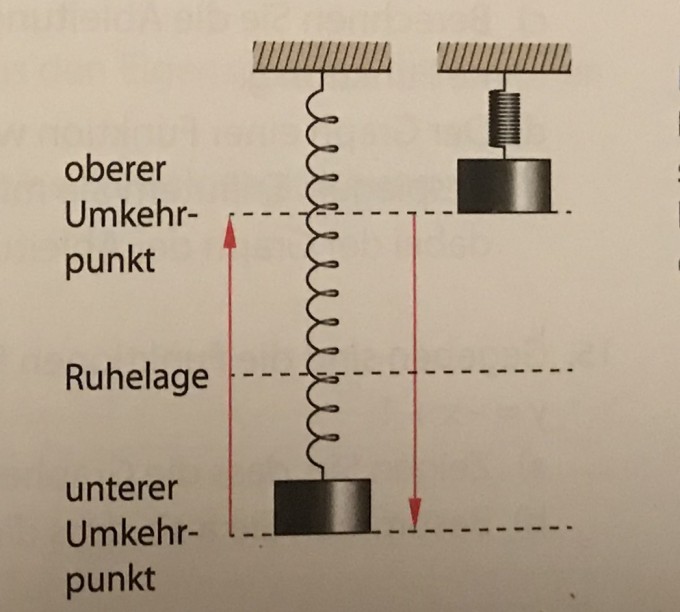
Die Funktion L(t)=-0.3•cos(6t) beschreibt die momentane Auslenkung eines Federpendels (t: Zeit in Sekunden, L(t): Auslenkung in Meter). Zum Zeitpunkt t = 0 wird das Pendel am unteren Umkehrpunkt losgelassen. Die momentane Geschwindigkeit wird durch v(t) = L‘(t) und die momentane Beschleunigung durch a(t) = L‘‘(t) angegeben.
a) Berechnen Sie die maximale Geschwindigkeit sowie den Zeitpunkt, zudem diese zum ersten Mal erreicht wird.
b) Berechnen Sie die Dauer einer Schwingungsperiode, indem Sie den Zeitunterschied zwischen zwei identischen Zuständen der Feder berechnen.
c) Berechnen Sie, wann die Beschleunigung den Wert null hat, und vergleichen Sie das Ergebnis mit dem aus a).
Problem/Ansatz:
 Ich verstehe Sachaufgaben allgemein nicht und bräuchte Hilfe. Zu a) habe ich die Nullstelle ausgerechnet 0,523599•(n1-0,5). Wenn ich 1 und 2 eingesetzt habe, kamen die Punkte P1(0,26|0) und P2(0,78|0) raus. Ich brauche dann ja die erste Ableitung und wenn ich 0,26 z.B. in die erste Ableitung einsetze, kommt 1,7999 raus. Stimmt das? Und wie komm ich bei b) und c) weiter?
Ich verstehe Sachaufgaben allgemein nicht und bräuchte Hilfe. Zu a) habe ich die Nullstelle ausgerechnet 0,523599•(n1-0,5). Wenn ich 1 und 2 eingesetzt habe, kamen die Punkte P1(0,26|0) und P2(0,78|0) raus. Ich brauche dann ja die erste Ableitung und wenn ich 0,26 z.B. in die erste Ableitung einsetze, kommt 1,7999 raus. Stimmt das? Und wie komm ich bei b) und c) weiter?