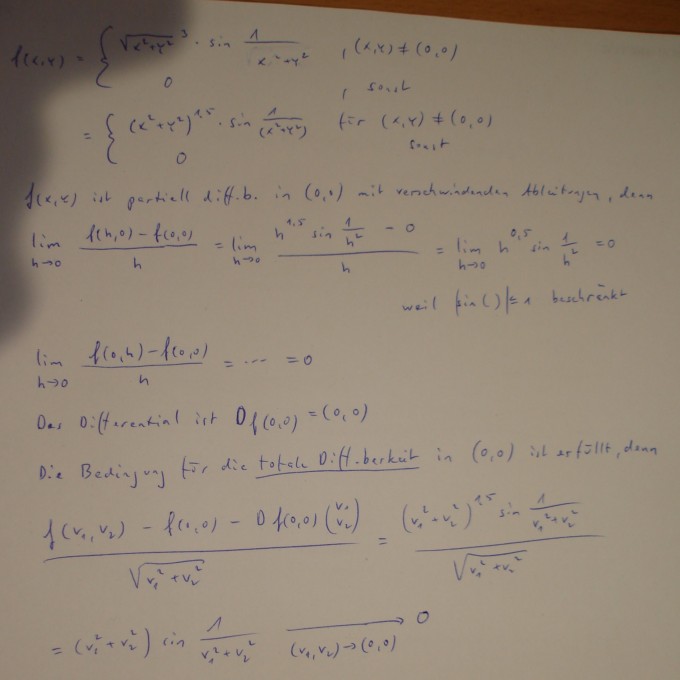
Missverständnis: R1→ R1
1. Schreibe ohne Betrag:
f(x)={x3 sin(1/x2) für x>0
f(x)={-x3 sin(1/x2) für x<0
f(x)={0 für x=0
Die einzige kritische Stelle ist x=0.
2. Weise die Stetigkeit nach: \( \lim\limits_{h\to0} \) f(h)=\( \lim\limits_{h\to0} \) f(h)=f(0) (lim von links und von rechts)
h>0 h<0
\( \lim\limits_{h\to0} \) f(h) = h3 sin(1/h2)=0, weil I sin(1/h2) I≤1, beschränkt
h>0
dasselbe für h<0 und h=0 machen, jedesmal kommt 0 raus, deshalb Stetigkeit
3. Bilde den Differentialquotienten:
\( \lim\limits_{h\to0} \) \( \frac{f(0+h)-f(0)}{h} \) =\( \lim\limits_{h\to0} \) \( \frac{h3 sin(1/h2)-0}{h} \)=\( \lim\limits_{h\to0} \) \( \frac{h2 sin(1/h2)-0}{1} \)=0, wie oben
h>0
dasselbe für h<0 machen, jedesmal kommt 0 raus, deshalb Differenzierbarkeit
Wenn die Abb. wirklich aus R2 → R1 gehen soll, muss man alles umschreiben:
f(x,y) = {(x2 +y2)1,5 sin (x2 +y2)-1 für (x,y) ≠ (0,0)
{ 0 sonst
Hieß die Aufg. dann: Weise die totale Diff.barkeit in (0,0) nach?
Dann so wie ganz oben!