Konstruiere die Hyperbel!

Question

Aufgabe:

Konstruiere eine Hyperbel mit [a=2, e=4]!

Problem/Ansatz:

Ich habe das achsenparallele Rechteck konstruiert, indem ich zuerst a, dann einen Strahl b dazu und e dann abgeschlagen habe (rechtwinkeliges Dreieck) -> somit gilt ja auch der pythagoräische Lehrsatz e^2=a^2+b^2. Dann habe ich die Asymptoten eingezeichnet, die durch die vier Eckpunkte gehen. Ich weiß dann aber leider nicht, wie ich die Schnittpunkte für die Äste (Hyperbel) bekomme...

A hat ja die Koordianten A(2|0), A'(-2|0)

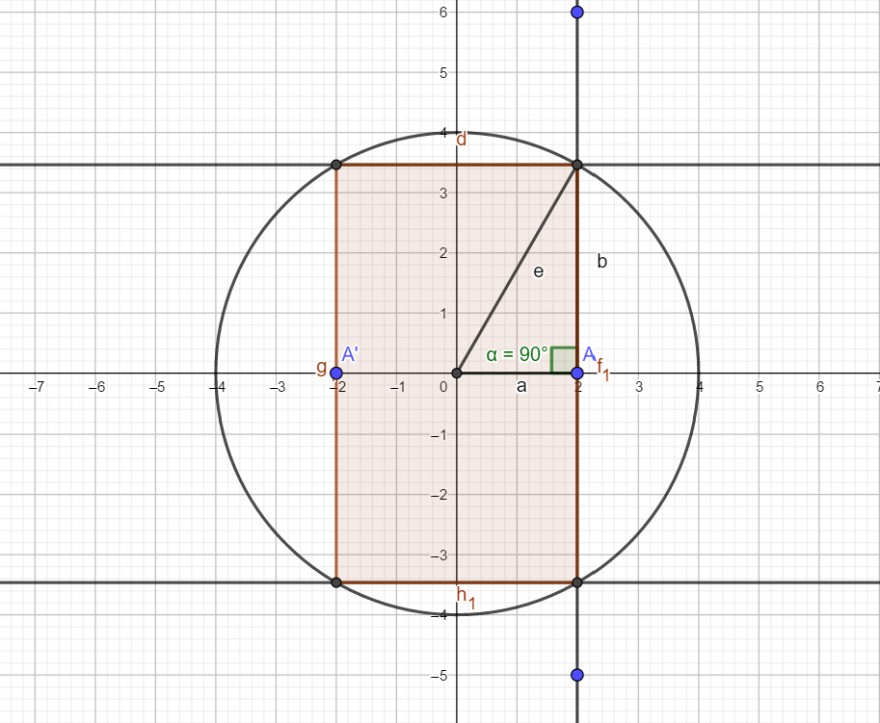
Text erkannt:

( 4)

 Vielen Dank im Voraus!

Answer 1

Hilft dir dieses Bild weiter?

Comments

Danke, werde es mir mal ansehen... und studieren!

Answer 2

a=2, e=4

$$\sqrt{(x-e)^2+y^2}-\sqrt{(x+e)^2+y^2} =\pm2a$$

$$\sqrt{(x-4)^2+y^2}-\sqrt{(x+4)^2+y^2} =\pm4$$

Die Schnittpunkte des Kreises mit der x-Achse sind die Brennpunkte F und F'.

Verbinde einen der  Schnittpunkte S zwischen Hyperbel und Kreis mit den Punkten F und F'. Du erhältst ein rechtwinkliges Dreieck. Den Abstand FS nenne ich z.

Dann gilt: z²+(z+4)²=8²

Berechne z≈3,2915. Zeichne zwei Kreisbögen mit dem Radius z und den Mittelpunkten F und F' und du erhältst S.

Comments

Danke, für die ausführliche Antwort... Wie kommt man aber auf die Hyperbel, die du schon eingezeichnet hast?

---

Bei einer Hyperbel liegen die Punkte doch so, dass die Differenz der Abstände von den Brennpunkten konstant ist, in deiner Aufgabe 4cm.

Also brauchst du eine beliebig lange Strecke, die z. B. 7cm lang ist, und eine um 4cm kürzere Strecke, die also 3cm lang wäre. Nun musst du die Punkte finden, die von einem Brennpunkt 7cm und vom anderen Brennpunkt 3cm entfernt sind. Dazu zeichnest du Kreisbögen mit den entsprechenden Radien.

Die Österreicher haben es hier ausführlich erklärt.

https://www.mathe-online.at/lernpfade/Kegelschnitte/?kapitel=4

---

Okay, danke!