Flächenberechnung bei Integralen

Question

Kann mir jemand zeigen wie ich folgende Aufgaben berechnen kann?

Es soll berechnet werden welchen Flächeninhalt die der jeweilige Graph mit der x-Achse einschließt.


a.) f:x → x^4-10x^2+9


b.) g:x → 0,5x^5-2x^3


 

Answer 1

Ohne die Angabe von Integrationsgrenzen dürfte das eine unendlicher Flächeninhalt sein.

Comments

Naja die Begrenzung ist ja von der x-Achse gegeben. Soll ja nur die Eingeschlossene Fläche der jeweiligen Funktion mit der x-Achse berechnet werden.

Answer 2

hi

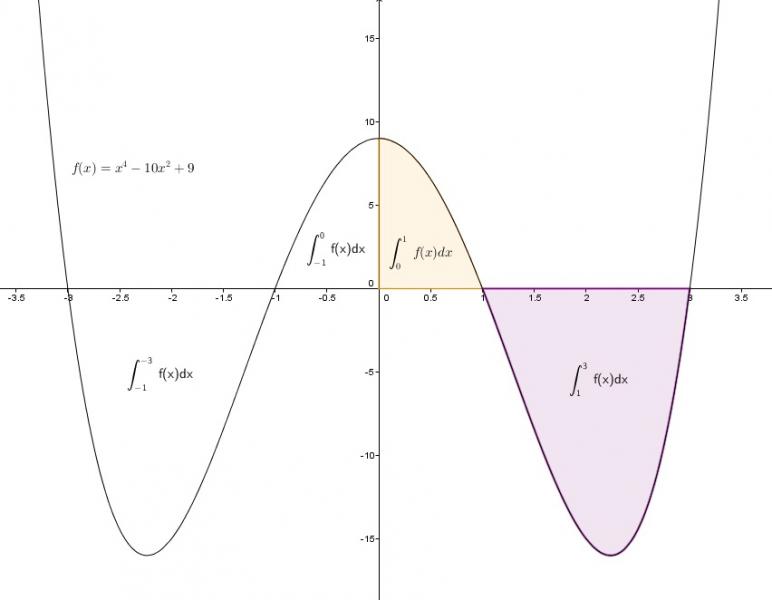
\( a) \\ f(x) = x^4-10x^2+9 \\ Nullstellen\\ x^4-10x^2+9 = 0 \\ z = x^2 \\ z^2-10z +9 = 0 \\ z_{1,2} = 5 \pm \sqrt{25-9} = 5 \pm 4\\ z_1 = 9, z_2 = 1\\ x = \sqrt{z} \\ x_{1,2}= \pm 3\\ x_{2,3}= \pm 1\\ f(x) = x^4-10x^2+9 \\ \int f(x)\mathrm{d}x = \frac{x^5}{5} - 10\frac{x^3}{3} + 9x + C \\ \int_{0}^{1}f(x)\mathrm{d}x = \int_{-1}^{0}f(x)\mathrm{d}x   \\ \int_{1}^{3}f(x)\mathrm{d}x  = -\int_{-1}^{-3}f(x)\mathrm{d}x \\ A = 2\int_{0}^{1}f(x)\mathrm{d}x + 2\left |\int_{1}^{3}f(x)\mathrm{d}x \right |\\ A = 2 \left [ \frac{x^5}{5} - 10\frac{x^3}{3} + 9x \right ]^1_0 + 2\left |\left [ \frac{x^5}{5} - 10\frac{x^3}{3} + 9x \right ]^3_1 \right | \\ A = 2 \cdot \frac{88}{15}+2\cdot \left | -\frac{304}{15} \right | = 2\cdot \frac{88+304}{15} = \frac{784}{15} \approx 52,267\\ \)

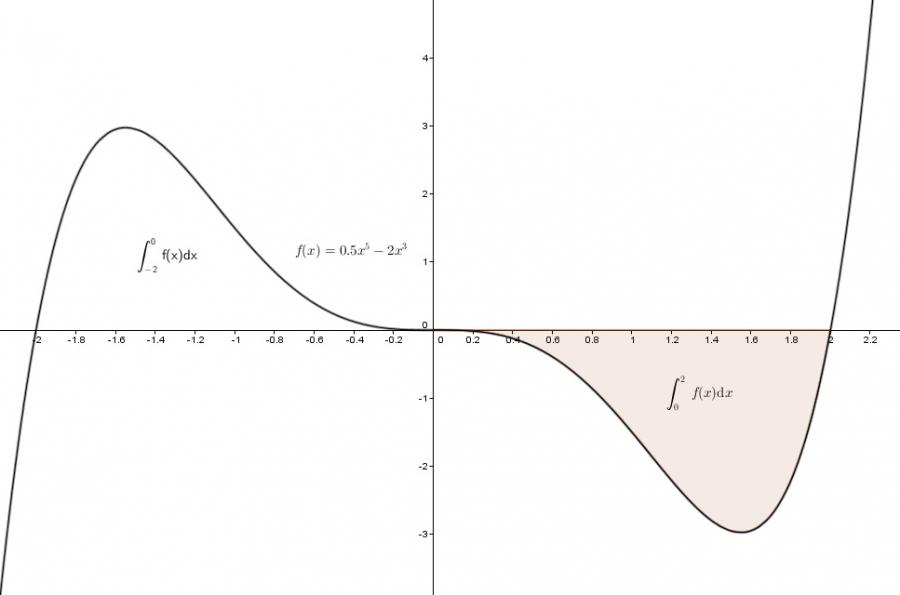
\( b) \\ f(x) = 0.5x^5 - 2x^3 \\ Nullstellen \\ 0.5x^5 - 2x^3 = 0 \\ 0.5x^3(x^2-4) = 0 \\ x_1 = 2, x_2 = -2 \\ \int f(x)\mathrm{d}x = 0.5\frac{x^6}{6}-2\frac{x^4}{4} + C = \frac{x^6-6x^4}{12} + C\\ A = 2\left |\int_{0}^{2} f(x)\mathrm{d}x  \right | A = \left |\left [ \frac{x^6-6x^4}{12}  \right ]_0^2 \right | \\ A = 2\cdot\left | -\frac{32}{12} \right | = \frac{32}{6} \approx 5.33 \)