Schnittwinkel von Gerade und Ebene

Question

Aufgabe:

mein Richtungsvektor ist (-12/6/-15) und

mein Normalvektor (1/0/1)

cos fi = -27: Wurzel aus 810

dann komme ich aber auf einen Schnittwinkel von  161,57 Grad.

Kann das stimmen?

Comments

Entweder 90° - arccos(phi) oder direkt den Sinus benutzen. Das ist auch das übliche Vorgehen für Gerade-Ebene.

---

Entweder 90° - arccos(phi) oder direkt den Sinus benutzen.

Sicher ?

Answer 1

sin(φ)= \( \frac{abs[\begin{pmatrix} -12\\6\\-15 \end{pmatrix}*\begin{pmatrix} 1\\0\\1 \end{pmatrix}]}{\begin{pmatrix} -12\\6\\-15 \end{pmatrix}*\begin{pmatrix} 1\\0\\1 \end{pmatrix}} \) = +27/√810 = 0,9486....

Im Zähler sollte der Betrag stehen, da verschiedene Winkel als Schnittwinkel definiert werden könnten, aber als Schnittwinkel immer der kleinstmögliche in Frage kommende bezeichnet wird.

φ = +71,56...^o

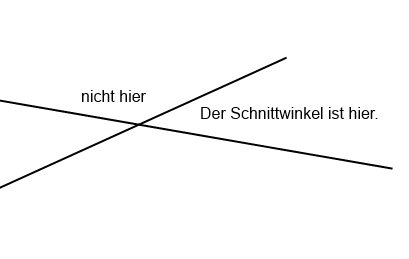
Ohne Betrag käme raus: sin(φ)= -0,9486.....

Damit wäre φ_k,1 = 251,56..^o + k*360^o, k∈ℤ und φ_k,2 = 288,43...^o + k*360^o, k∈ℤ

Der Winkel φ_-1,2 = -71,56...^o, aber nicht +71,56...^o

Comments

Zeichnung ergänzt.

Answer 2

ARCSIN([-12, 6, -15]·[1, 0, 1]/(ABS([-12, 6, -15])·ABS([1, 0, 1]))) = -71.57°

Der Winkel beträgt ca. 71.57°.

Die 161.57° ist der Winkel zwischen dem Normalenvektor und dem Richtungsvektor der Geraden. Das ist aber nicht der Winkel zwischen Gerade und Ebene. Dazu müsstest du noch

90° - 161.57° = -71.57°

rechnen. Und das ist auch das was ich heraus habe.