Verständnisfrage Polynomfunktion

Question

Aufgabe:

Text erkannt:

11

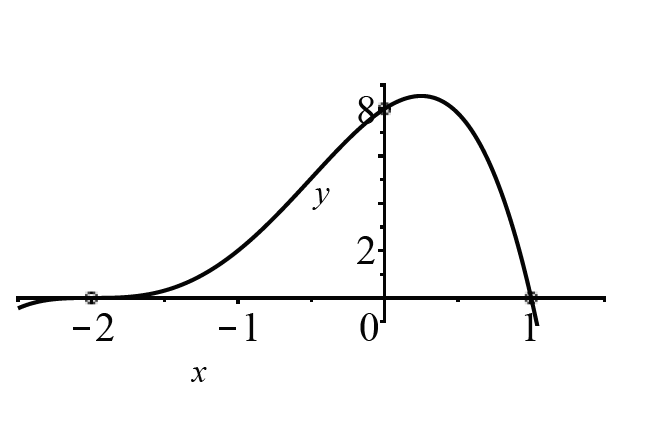
Bestimmen Sie die Koeffizienten des Polynoms p(x) mit dem Grad 4.

Problem/Ansatz:

.., ich habe wieder einmal eine Verständnisfrage. Ich weiss, wie ich diese Polynomfunktion berechne, jedoch ist mir da wieder eine Frage aufgetaucht, die mich seit einiger Zeit beschäftigt.

Man hat ja die Nullstellen -2 und 1 und den Grad -> a(x+2)^3(x-1) Also kann ich hier einfach P(0) = 8 einsetzen und a ausrechnen, was mir dann -1 gibt. Ich verstehe jedoch nicht ganz genau, was diese "a" darstellt. Wenn ich diese Unbekannte berechne, was habe ich dann genau von der Polynomfunktion berechnet?

Vielleicht denke ich viel zu weit, könnte mir da jemand auf die Sprünge helfen?

Answer 1

Wenn du für a verschiedene Werte einsetzt, wird die Kurve in y-Richtung gestreckt. Durch den y-Achsenabschnitt 8 wird a dann festgelegt.

Comments

Ist das eigentlich der gleiche Grund wieso man bei einer Stammfunktion noch +k macht, weil man den Funktion eigentlich unendlich verschieben könnte. Das heisst mit a definiere ich einen Graphen, der genau P(0) = 8 beinhaltet.

---

Bei Stammfunktionen muss die Steigung ja an einer Stelle immer gleich sein. Deshalb kann man die Kurve beliebig in y-Richtung verschieben, was dem +C entspricht.

Answer 2

Es gibt ja viele Polynomfunktionen 4. Grades, die bei -2 einen Sattelpunkt und bei 1

eine Nullstelle haben.  Offenbar unterscheiden die sich

alle um einen Faktor, der wohl sowas wie Strecken in y-Richtung bewirkt.

Mit der zusätzlichen Rechnung hast du einen davon ausgewählt.

Answer 3

Der Ablauf einer " Steckbriefaufgabe " für Polynome
ist immer derselbe. Angaben aufschreiben
f ( -2 ) = 0 | Koordinaten
f ´( -2 ) = 0 | Steigung
f ´´ ( -2 ) = 0 | Krümmung
f ( 0 ) = 8 | Koordinaten
f ( 1 ) = 0 | Koordinaten
5 Angaben = Funktion 4.Grades
f ( x ) = a * x^4 + b * x^3 + c * x^2 + d * x + e
Was wird sonst noch gebraucht um alle Angaben
verwerten zu können
1.Ableitung und 2.Ableitung
f ´( x ) = 4a * x^3 + 3b * x^2 + 2c * x + d
f ´´( x ) = 12a * x^2 + 6b * x + 2c
Einsetzen der Angaben in die Funktion
f ( -2 ) = 0 | Koordinaten
f ´( -2 ) = 0 | Steigung
f ´´ ( -2 ) = 0 | Krümmung
f ( 0 ) = 8 | Koordinaten
f ( 1 ) = 0 | Koordinaten
f ( -2 ) = a * (-2)^4 + b * (-2)^3 + c * (-2)^2 + d * (-2) + e = 0
f ´( -2 ) = 4a * (-2)^3 + 3b * (-2)^2 + 2c * (-2) + d = 0
f ´´( -2 ) = 12a * (-2)^2 + 6b * (-2) + 2c = 0
f ( 0 ) = a * 0^4 + b * 0^3 + c * 0^2 + d * 0 + e = 8

f ( 1 ) = a * 1^4 + b * 1^3 + c * 1^2 + d * 1 + e = 0

a * (-2)^4 + b * (-2)^3 + c * (-2)^2 + d * (-2) + e = 0
4a * (-2)^3 + 3b * (-2)^2 + 2c * (-2) + d = 0
12a * (-2)^2 + 6b * (-2) + 2c = 0
a * 0^4 + b * 0^3 + c * 0^2 + d * 0 + e = 8
a * 1^4 + b * 1^3 + c * 1^2 + d * 1 + e = 0

Jetzt das lineare Gleichungssystem lösen.

Steckbriefrechner im Internet
f(x) = -x^4 - 5·x^3 - 6·x^2 + 4·x + 8

Bin gern weiter behilflich

Answer 4

Man hat ja die Nullstellen -2 und 1 und den Grad -> a*(x+2)^3*(x-1). Also kann ich hier einfach P(0) = 8 einsetzen und a ausrechnen, was mir dann -1 gibt.

Der Ansatz ist sehr gut und richtig.

Ich verstehe jedoch nicht ganz genau, was diese "a" darstellt. Wenn ich diese Unbekannte berechne, was habe ich dann genau von der Polynomfunktion berechnet?

Mit \(a=-1\) kannst du \(a\cdot (x+2)^3\cdot (x-1)\) ausmultiplizieren und bist fertig.