Doch wie sieht es bei einem Winkel von beispielsweise 150° aus?
Wie kommt die Wurzel da in den Zähler?
Ich hatte die Aufgabe 2) so verstanden, dass der Winkel gesucht ist, dessen Cosinus \(=-\sqrt 3 /2\) ist. Also formal:$$\cos \alpha = -\frac 12 \sqrt 3$$und \(\alpha\) ist gesucht. Ist das richtig?
Auf Deine Frage: "Wie kommt die Wurzel da in den Zähler?" kann man dann nur antworten: das war die Aufgabenstellung!
Sollte ich doch richtig liegen, so geht man hier mit Hilfe des Einheitskreises wie folgt vor: man zeichnet eine senkrechte Gerade im Abstand des gegebenen Wertes von der Y-Achse.
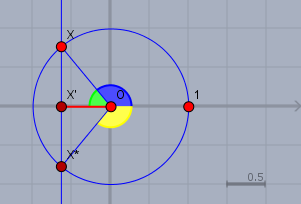
Der Cosinus ist das Verhältnis von Ankathete zu Hypotenuse. I, Dreieck \(\triangle X'OX\) ist die Hypotenuse \(|XO|\) immer \(=1\) (wg. Einheitskreis). Folglich ist der Cosinus des blauen Winkels die rot markierte Strecke.
Diese senkrechte Gerade schneidet den Einheitkreis in den Punkten \(X\) und \(X^*\). Der - bzw. die beiden - gesuchten Winkel sind der blaue und der gelbe. Da die ganze Figur symmetrisch zur X-Achse ist, unterscheiden sich diese beiden Winkel nur im Vorzeichen.
Um heraus zu bekommen, wie groß die Winkel sind, kann man nun z.B. das Dreieck \(\triangle X'OX\) betrachten. Dies ist ein rechtwinkliges und damit gilt nach Pythagoras:$$|X'O|^2 + |X'X|^2 = |XO|^2$$die rote Strecke (\(=|X'O|\)) soll lt. Aufgabenstellung gleich \(-\sqrt 3 /2\) sein, \(|XO|\) ist immer \(=1\), da es sich hier um den Einheitskreis handelt. Dann ist \(|X'X|\):$$|X'X| = \sqrt{|XO|^2 - |X'O|^2} = \sqrt{1 - \left( \frac 12 \sqrt 3\right)^2} = \sqrt{1 - \frac 34} = \frac 12$$dann ist wegen der Symmetrie \(|X^*X'|\) auch gleich \(=1/2\) und \(|X^*X|=1\). Somit ist \(\triangle X^*OX\) ein gleichseitiges Dreieck, in dem alle Winkel \(=60°\) groß sind. Und wieder wegen der Symmetrie ist der grüne Winkel genau halb so groß - also \(=30°\). Der blaue Winkel \(\alpha\) ist der Nebenwinkel des grünen und folglich ist$$\alpha = 180° - 30° = 150°$$Bleibt noch der gelbe Winkel mit \(-150°\) (s.o.).
Aus dieser Überlegung folgt schlußendlich:$$\cos(150°) = \cos(-150°) = - \frac 12 \sqrt 3$$Falls Du Fragen hast, so melde Dich bitte.
Gruß Werner
