Einheitskreis: Wie komme ich rein rechnerisch auf die Kosinuswerte?

Question

Aufgabe:

Wie komme ich rein rechnerisch auf die Kosinuswerte?

1) Sei der Winkel 120° gegeben.

2) Sei der Wert $- \frac{ \sqrt{3}}{2}$

3) Wie kann ich nur mit gegebenen Werten ein Dreieck in einem Graphen zeichnen?

Problem/Ansatz:

$\begin{array}{|c|c|c|c|c|c|c|c|}\hline \alpha & {0^{\circ}} & {30^{\circ}} & {45^{\circ}} & {60^{\circ}} & {90^{\circ}} & {120^{\circ}} & {135^{\circ}} & {150^{\circ}} & {180^{\circ}} \\ \hline x & 0 & {\frac{\pi}{6}} & {\frac{\pi}{4}} & {\frac{\pi}{3}} & {\frac{\pi}{2}} & {\frac{2\pi}{3}} & {\frac{3 \pi}{4}} & {\frac{5 \pi}{6}} & {\pi} \\ \hline \operatorname{cos\alpha} & {1} & {\frac{\sqrt{3}}{2}} & {\frac{\sqrt{2}}{2}} & {\frac{1}{2}} & {0} & {-\frac{1}{2}} & {-\frac{\sqrt{2}}{2}} & {-\frac{\sqrt{3}}{2}} & {-1} \\ \hline \end{array}$

Answer 1

Hallo Cron,

wie komme ich rein rechnerisch auf die cosinus-Werte?

nicht rechnen, sondern den Einheitskreis anschauen und den Winkel bzw. den Cosinuswert eintragen. Mit einem Winkel von 120° ergibt sich folgendes Bild:

Der Winkel $120°$ ist der blau markierte und der Cosinus dieses Winkels ist die rote Strecke vom Ursprung bis zum Fußpunkt $X'$ von $X$ auf der X-Achse. Das gelblich markierte Dreieck ist ein gleichseitiges, da der Nebenwinkel von $120°$ gleich $60°$ ist, und $X'$ halbiert demzufolge die Strecke von $-1$ bis $O$ - also ist $$\cos(120°) = - \frac 12$$negativ, weil sie nach links in den negativen Bereich hinein geht.

Welcher Winkel ergibt einen Cosinus von $-\sqrt 3/2$? Dazu zeichne den Einheitskreis und eine vertikale Gerade im Abstand von $-\sqrt 3 / 2$ parallel zur Y-Achse. Die schneidet den Einheitskreis bei $X$ und $X^*$.

Der Wert $-\sqrt 3/2$ ist genau die Höhe in einem gleichseitigen Dreieck mit der Kantenlänge $1$. Folglich ist das gelb markierte Dreieck wieder ein gleichseitiges. Und da die X-Achse den Winkel von $60°$ genau halbiert gilt: $$\cos\left( 180° - \frac{60°}2\right) = \cos(150°) = \cos(-150°) = - \frac 12 \sqrt 3$$

3) Wie kann ich nur mit gegebenen Werten ein Dreieck in einem Graphen zeichnen?

Die Frage verstehe ich nicht, Welche Werte sind gegeben? Und wie soll das Dreieck in welchem Graphen liegen?

Gruß Werner

Comments

Sehr schön dargestellt.

Welches Zeichentool hast du dafür verwendet? Man muss ja manchmal etwas zeichen zum besseren Erklären, aber Geozeichner 2D ist dazu oft nicht gut geeignet.

---

Welches Zeichentool hast du dafür verwendet?

Ich verwende das Geometrie-Programm Cinderella -> cinderella.de

---

Hallo Werner,

Vielen Dank Werner für die Ausführung.
Die Werte mit den Wurzeln sorgen bei mir für Verwirrung.

Zu1) 120° ist für ich nun verständlich. Doch wie sieht es bei einem Winkel von beispielsweise 150° aus?
Wie kommt die Wurzel da in den Zähler?

Und wie errechnet man sich denn genau:
$\cos \left(-150^{\circ}\right)=-\frac{1}{2} \sqrt{3}$

Zu 3) Es ging mir hierbei um die bei Punkt 1 und 2 bereits dargestellten Grafiken.

---

Doch wie sieht es bei einem Winkel von beispielsweise 150° aus?
Wie kommt die Wurzel da in den Zähler?

Ich hatte die Aufgabe 2) so verstanden, dass der Winkel gesucht ist, dessen Cosinus $=-\sqrt 3 /2$ ist. Also formal:$$\cos \alpha = -\frac 12 \sqrt 3$$und $\alpha$ ist gesucht. Ist das richtig?

Auf Deine Frage: "Wie kommt die Wurzel da in den Zähler?" kann man dann nur antworten: das war die Aufgabenstellung!

Sollte ich doch richtig liegen, so geht man hier mit Hilfe des Einheitskreises wie folgt vor: man zeichnet eine senkrechte Gerade im Abstand des gegebenen Wertes von der Y-Achse.

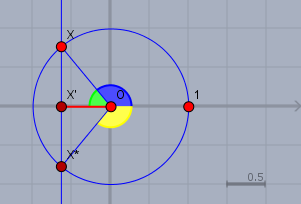
Der Cosinus ist das Verhältnis von Ankathete zu Hypotenuse. I, Dreieck $\triangle X'OX$ ist die Hypotenuse $|XO|$ immer  $=1$ (wg. Einheitskreis). Folglich ist der Cosinus des blauen Winkels die rot markierte Strecke.

Diese senkrechte Gerade schneidet den Einheitkreis in den Punkten $X$ und $X^*$. Der - bzw. die beiden - gesuchten Winkel sind der blaue und der gelbe. Da die ganze Figur symmetrisch zur X-Achse ist, unterscheiden sich diese beiden Winkel nur im Vorzeichen.

Um heraus zu bekommen, wie groß die Winkel sind, kann man nun z.B. das Dreieck $\triangle X'OX$ betrachten. Dies ist ein rechtwinkliges und damit gilt nach Pythagoras:$$|X'O|^2 + |X'X|^2 = |XO|^2$$die rote Strecke ($=|X'O|$) soll lt. Aufgabenstellung gleich $-\sqrt 3 /2$ sein, $|XO|$ ist immer $=1$, da es sich hier um den Einheitskreis handelt. Dann ist $|X'X|$:$$|X'X| = \sqrt{|XO|^2 - |X'O|^2} = \sqrt{1 - \left( \frac 12 \sqrt 3\right)^2} = \sqrt{1 - \frac 34} = \frac 12$$dann ist wegen der Symmetrie $|X^*X'|$ auch gleich $=1/2$ und $|X^*X|=1$. Somit ist $\triangle X^*OX$ ein gleichseitiges Dreieck, in dem alle Winkel $=60°$ groß sind. Und wieder wegen der Symmetrie ist der grüne Winkel genau halb so groß - also $=30°$. Der blaue Winkel $\alpha$ ist der Nebenwinkel des grünen und folglich ist$$\alpha = 180° - 30° = 150°$$Bleibt noch der gelbe Winkel mit $-150°$ (s.o.).

Aus dieser Überlegung folgt schlußendlich:$$\cos(150°) = \cos(-150°) = - \frac 12 \sqrt 3$$Falls Du Fragen hast, so melde Dich bitte.

Gruß Werner