Ableitung von ln mit Wurzel im Nenner und Multiplikation im Zähler des Bruches

Question

Aufgabe:

Ich möchte folgende Funktion ableiten:

ln( \( x*a^{x} \) / \( \sqrt{1+x^2} \)  

Problem/Ansatz:

Meine Rechnung:

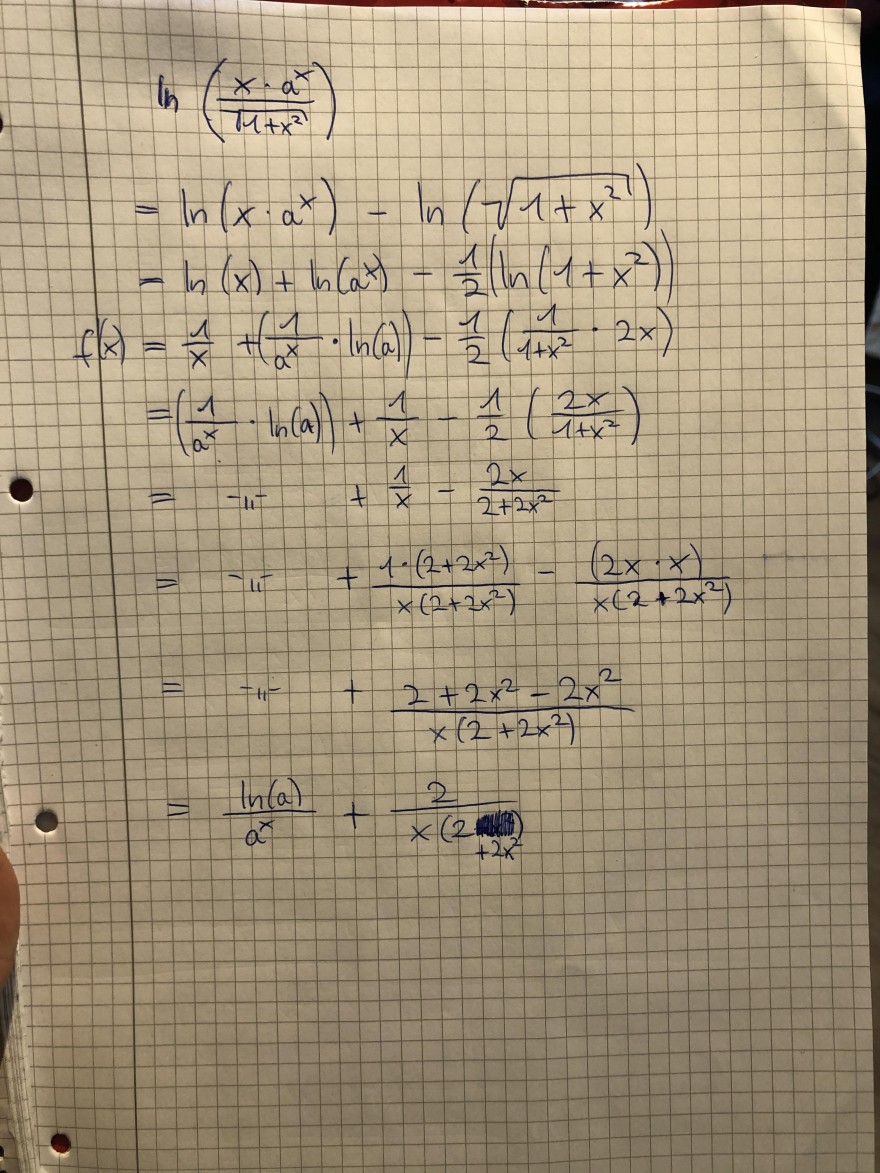
Text erkannt:

$$ \begin{array}{l} {\quad \ln \left(\frac{x \cdot a^{x}}{11+x^{2}}\right)} \\ {=\ln \left(x \cdot a^{x}\right)-\ln (\sqrt{1+x^{2}})} \\ {=\ln \left(x \cdot a^{x}\right)-\frac{1}{2}\left(1+x^{2}\right)} \\ {-\ln (x)+\ln \left(a^{x}\right)-\frac{1}{2}\left(\ln \left(1+x^{2}\right)\right)} \\ {=\frac{1}{x}+\left(\frac{1}{a^{x}} \cdot \ln (a)\right)-\frac{1}{2}\left(\frac{1}{1+x^{2}} \cdot 2 x\right)} \\ {=\frac{1}{x}+\left(\frac{1}{a^{x}} \cdot \ln (a)\right)-\frac{1}{x}-\frac{1}{2}\left(\frac{2 x}{1+x^{2}}\right)} \\ {=-\frac{1}{x^{2}} \cdot \ln (a) |+\frac{1}{x}-\frac{1}{2}\left(\frac{2 x}{1+x^{2}}\right)} \\ {=-\frac{1}{x^{2}} \cdot \ln (a) |+\frac{1}{x\left(2+2 x^{2}\right)}-\frac{(2 x \cdot x)}{x\left(2+2 x^{2}\right)}} \\ {=-\frac{1}{x}+\frac{2+2 x^{2}-2 x^{2}}{x\left(2+2 x^{2}\right)}} \end{array} $$
\( 0=\frac{\ln (a)}{a^{x}}+\frac{2}{x(2 a+2)^{2}} \)

 Dies ist die Lösung nach dem Ableitungsrechner im Internet:

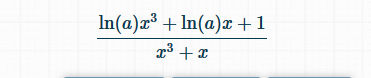
Ich scheine etwas massiv falsch zu machen, ich bitte um Hilfe. Vielen Dank im Voraus!!

Text erkannt:

\( \frac{\ln (a) x^{3}+\ln (a) x+1}{x^{3}+x} \)

Answer 1

Bei dir ist die Ableitung von a^x einfach nur ln(a). Das stimmt aber nicht.

Du kannst übrigens (vor dem Ableiten) ln(a^x) einfacher als x*ln(a) schreiben. Das vereinfacht das Ableiten...

Beim hinteren Bruch machst du dir es selbst unnötig schwer, indem du den Bruch tatsächlich mit 1/2 multiplizierst.

Warum kürzt du nicht gleich die 2 im Zähler mit der 2 im Nenner des Faktors 1/2?