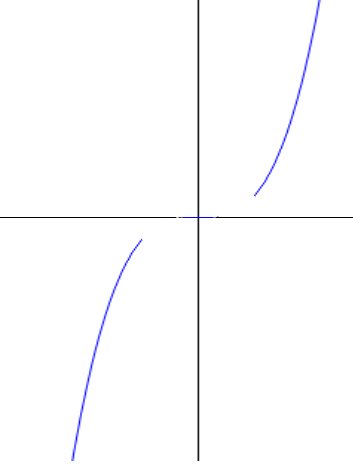
Wenn man nur benutzt, dass die Funktion für x>2 linksgekrümmt ist und für x<2 rechtsgekrümmt ist, folgt, dass ein N∈ℕ ex, so dass f(x) streng monoton ist für alle x>N und x<-N.
Wenn man zusätzlich das Wissen reinsteckt, dass f(x) eine ganzrat. Fkt 3. Grades sein muss, folgt, dass ein N∈ℕ ex, so dass f(x) entweder streng monoton fallend ist für alle x>N und für alle x<-N oder dass f(x) streng monoton steigend ist für alle x>N und für alle x<-N.
Wenn man auch noch reinsteckt, dass f(x) eine ganzrat. Fkt 3. Grades sein muss mit positivem Koeff. vor der höchsten Potenz, da das VZ der Koeff. beim Ableiten ganzrat. Funktionen erhalten bleibt, folgt, dass f(x) streng monoton steigend ist für alle x>N und für alle x<-N.